Lista 8 – Sem campus – Calculo – Funções de uma variável – Lista FUV-MADMAT – questão 6 item d
Dada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
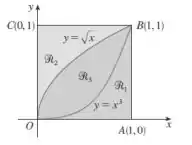
- ao longo de BC
Passo 1
Faaaaaala, galera... Tranquileba??? Bora Responder Aí essa questão
Sabemos que o volume pode ser dado por:
Bora pro próximo passo?
Passo 2
Obrigado por vir
A função A(x) ao longo de BC compreende y=1, logo temos que fazer y=1 até que ele chegue a 0, por rotação, certo? Logo:
Mas
Passo 3
X compreende de [0,1]
Assim:
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .