Lista 8 – Sem campus – Calculo – Funções de uma variável – Lista FUV-MADMAT – questão 2 item g
Esboce a região delimitada pelas curvas e decida se a integração deve ser feito com relação a variável x ou y. Desenhe um retângulo típico com sua altura e largura. Finalmente ache a área de integração.
g)
Passo 1
Faaaaaala, galera... Tranquileba??? Bora Responder Aí essa questão
Seguinte... Temos, das funções dadas, o seguinte gráfico.
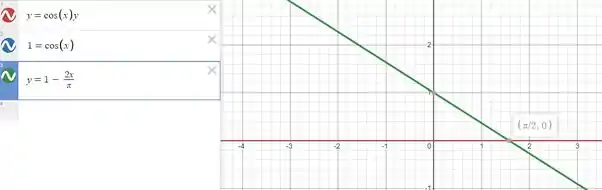
É notável que seria muito mais fácil se fizéssemos a integração com respeito ao eixo x né?! Se não fosse assim teríamos que trocar a função pro eixo y, redefinir os limites e aquela bagunça toda...
Bora pro próximo passo?
Passo 2
Obrigado por vir
Assim... Bom, sabemos que temos a um triangulo típico, e sua área (que é o que vamos encontrar) é:
Mas se fosse assim seria muito fácil né... estamos aqui para dificultar, então? Hahahahaha.Não, mas para explicarmos de maneira precisa o que foi pedido, e nos foi pedido para fazermos por integração né? Então bora lá
Passo 3
A função então rege o gráfico é
E a área será dada por:
Bom, os limites a e b pra x vão de 0 até . Assim:
Resposta
A região esboçada está no passo 1.
A variável é sobre x
E a área.