Lista de exercícios 10 – UFABC – Técnicas de integração– questão 2 item d
Encontre o comprimento do arco do gráfico da equação dada entre os pontos P e Q ou no intervalo especificado.
d)
Passo 1
Faaaaaala, galera... Tranquileba?? Bora responder Aí essa questão?
Bom, pede-se o comprimento de um arco, ou seja, o comprimento da linha de uma função de um ponto até o outro.
E o comprimento do arco que queremos saber é esse:
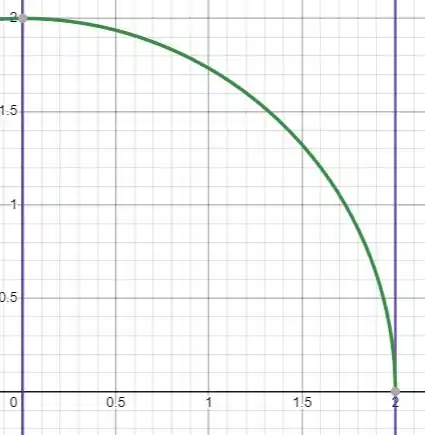
Que é a linha verde.
Duas coisas precisamos ter em mente quando queremos calcular o comprimento de um arco: saber derivar e a seguinte formula na qual aplicamos essa integração:
Onde é a função, “a” e “b” os limites de integração
Bom, já tendo a faca e o queijo na mão, vamos lá?
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Temos a função , e derivando usando a regra da cadeia:
Agora vamos aplicas essa derivada na nossa fórmula do comprimento do arco.
Vamos aplicar o limite dado:
Assim:
Podemos deixar isso mais bonito, né?! Veja:
Assim substituindo:
Passo 3
Geralmente essas integrais são resolvidas por uma substituição trigonométrica, geralmente são:
E variantes dessa, o que nos libera uma gama de opções.
Qual dessas que melhor se encaixa nesse caso?
Se escolheu escolheu certo, podemos fazer:
Derivando:
E quando fazemos uma substituição, qualquer que seja, os limites de interação devem acompanhar essa substituição, ou seja:
Assim a nossa equação fica:
Como dado antes
Tirando os termos que se cortam:
Portanto, o comprimento do arco vale unidades
Valeu, carinha.