Lista 8 – Sem campus – Calculo – Funções de uma variável – Lista FUV-MADMAT – questão 5
Determine c para que a região delimitada pelas parábolas e seja 576
Passo 1
Faaaaaala, galera... Tranquileba??? Bora Responder Aí essa questão
Antes, vamos fazer um gráfico de ambas as equações? Assim:
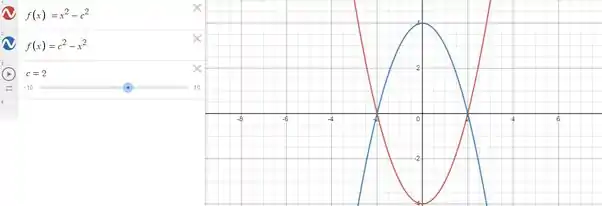
Onde c é o parâmetro que delimita a abertura entre as parábolas.
Veja que são simétricos, pois se igualarmos ambas as equações:
Temos que:
Bora pro próximo passo?
Passo 2
Obrigado por vir
Se é simétrico na parte de cima e na parte de baixo, então podemos fazer somente uma e multiplicar por 2, certo?!
Assim, peguemos a função em azul e aplicamos a integral. Bora?
Passo 3
Assim:
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x