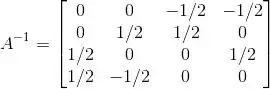Considere a matriz
Tal matriz é inversível? Em caso afirmativo, determine .
Passo 1
Lembra que a matriz A vai ser inversível se o determinante dela não for zero.
Então vamos começar calculando o determinante de A.
Pra fazer isso, vamos escalonar a matriz A lembrando que:
- Substituir uma linha pela soma dela com o múltiplo de outra linha não altera o determinante
- Trocar as linhas muda o sinal do determinante
- Multiplicar uma linha por escalar faz com que o determinante também fique multiplicado por esse escalar
Escalonando:
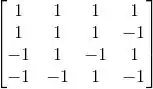
Note que B é uma matriz triangular superior, e o determinante de uma matriz desse tipo é o produto dos elementos da diagonal principal:
Como no escalonamento só fizemos operações que não alteram o determinante e duas operações de troca de linha (cada uma mudando o sinal do determinante uma vez), temos:
Logo, a matriz A é inversível!
Passo 2
Agora para calcular a inversa, escalonamos a matriz A completamente, junto com a matriz identidade do lado:
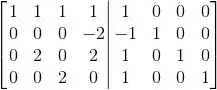
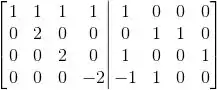
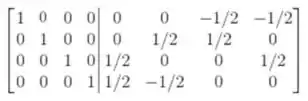
Portanto:
Resposta
É inversível:
Exercícios de Livros Relacionados
Seja A =1 - 1 - 4 1 .Mostraremos no Exemplo 6.6 na página 398 que P = 1 1 - 2 2 e D = 3 0 0 - 1 São tais que A = P D P - 1 .Determine A k , para k =1, 2, 3...
23. Sejam Ax=b um sistema de equações lineares consistente arbitrário e x1 uma solução fixada. Mostre que qualquer solução do sistema pode ser escrita na forma x=x1+x0, em que x0 é a solução de Ax=0.
Simplifique(A C^(- 1))^(- 1) (A C^(- 1)) (A C^(- 1))^(- 1) A D^(- 1)
Use o Teorema 1.4 . 5 para calcular a inversa da matriz A = ([[3,1],[5,2]])
Use o Teorema 1.4 . 5 para calcular a inversa da matriz D = ([[2,0],[0,3]])