UnB – Introdução à Álgebra Linear – Listas de IAL, Lista 1, 29
Mostre que é não-invertível para quaisquer valores das entradas.
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado pede pra gente mostrar que essa matriz não é invertível para qualquer valor das entradas. Ou seja, temos que mostrar que a matriz não possui inversa independentemente do valor das entradas , , , , , , e . Mas como fazemos isso?
Bom, para encontrar a inversa de uma matriz a gente pode aplicar o algoritmo da inversão, que diz pra gente operar até ela se transformar em . Então, vamos aplicar esse algoritmo e ver se dar certo.
Passo 2
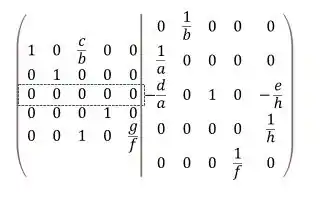
Galera, nós queremos reduzir à matriz identidade por operações com linhas e, simultaneamente, aplicar essas operações a para produzir . Para conseguir isso, juntamos a matriz identidade à direita de , com o que produzimos uma matriz da forma:
Então, temos
Vamos começar trocando a linha com a linha e a linha com a linha :
Agora vamos multiplicar a linha por e a linha por :
Em seguida, vamos multiplicar a linha por e a linha por :
Passo 3
Agora vamos tentar zerar os elementos abaixo do pivô da linha , multiplicado a linha por e somando na linha . Assim:
Agora vamos multiplicar a linha por e somar na linha :
Percebe que agora nós temos uma linha de zeros na matriz?
Isso torna nossa matriz singular, e uma matriz singular não possui inversa. Logo, mesmo sem conhecer os valores de , , , , , , e , nós podemos dizer que a matriz é não-invertível, como queríamos demonstrar.
Valeu, galera. Até a próxima! 😉