UnB – Introdução à Álgebra Linear – Listas de IAL, Lista 1, 28i
Encontre a inversa das matrizes:
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma matriz e pediu pra gente encontrar a inversa dessa matriz. Mas será que dá pra achar a inversa dessa matriz?
Se a gente olhar direitinho, vê que a terceira linha da matriz é composta só de zeros:
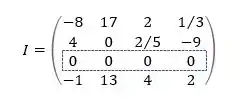
E aí, a gente precisa lembrar que uma matriz quadrada com uma linha ou coluna de zeros é chamada de singular. E uma matriz singular, por definição, não possui inversa e é dita não invertível.
É isso, galera. Até a próxima! 😉
Resposta
Exercícios de Livros Relacionados
Seja A =1 - 1 - 4 1 .Mostraremos no Exemplo 6.6 na página 398 que P = 1 1 - 2 2 e D = 3 0 0 - 1 São tais que A = P D P - 1 .Determine A k , para k =1, 2, 3...
23. Sejam Ax=b um sistema de equações lineares consistente arbitrário e x1 uma solução fixada. Mostre que qualquer solução do sistema pode ser escrita na forma x=x1+x0, em que x0 é a solução de Ax=0.
Simplifique(A C^(- 1))^(- 1) (A C^(- 1)) (A C^(- 1))^(- 1) A D^(- 1)
Use o Teorema 1.4 . 5 para calcular a inversa da matriz A = ([[3,1],[5,2]])
Use o Teorema 1.4 . 5 para calcular a inversa da matriz D = ([[2,0],[0,3]])