UFES. Álgebra Linear. Prova P2 Tarde. Questão 7b.
Determine se as afirmações abaixo são verdadeiras ou falsas. Justificando sua resposta.
(b) Se e são matrizes semelhantes, então .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Esse tipo de questão é muito interessante e bastante cobrado por nossos queridos profs, pois elas são ótimas para o aluno compreender alguns assuntos, então ter experiência nesse tipo de questão é uma baita vantagem para vir o 10 na prova!
Para essa questão, vamos julgar algumas afirmações, de acordo com nossa análise, dizer se a afirmação é verdadeira ou falsa e justificar a resposta.
Essa questão é bem rapidinha, então com essa breve introdução, podemos partir para o principal objetivo.
Passo 2
A afirmação que vamos julgar diz que “Se e são matrizes semelhantes, então ”.
Temos duas matrizes, a matriz e a matriz e elas são semelhantes, por isso, o determinante da matriz é igual o determinante da matriz .
Blz, mas o que são matrizes semelhantes? 🤔🤔
A definição de matrizes semelhantes é: “duas matrizes quadradas são semelhantes de existir uma matriz invertível, tal que ”
A partir dessa definição, podemos afirmar que as matrizes e são quadradas de ordem
Se e são semelhantes, há uma relação de equivalência, por exemplo: se é semelhante a , logo é semelhante a .
Uma matriz é semelhante a si mesma e por fim, se é semelhante a e é semelhante a , logo é semelhante a .
A partir das 7 propriedades de matrizes semelhantes, temos que:
1- é invertível apenas se também for.
2- e possuem o mesmo polinômio característico.
3- e tem os mesmos autovalores com a mesma multiplicidade.
4- e tem o mesmo traço.
5- e são semelhantes para todo .
6- As matrizes de um operador linear de dimensão finita são semelhantes.
7-
Podemos provar a propriedade 7 da seguinte maneira:
Se , então
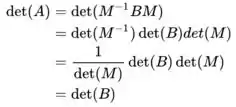
A partir dessa propriedade, podemos afirmar de o item b é verdadeiro.
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
Verdadeiro! ✔