Seja A uma matriz na forma
Onde cada representa um número diferente de zero. (Dois quadradinhos idênticos podem representar números diferentes). Então a inversa de A tem a forma:
(a)
(b)
(c)
(d)
Passo 1
Para resolver essa questão, vamos trocar os quadradinhos da matriz A por números quaisquer.
Agora vamos aplicar o processo pra obter a inversa de uma matriz: colocamos a matriz identidade do lado e escalonamos completamente.
Passo 2
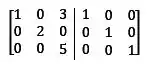
A matriz já é diagonal superior, então agora a gente só precisa transformar a matriz do lado esquerdo na identidade através de operações elementares.

Passo (i):
Passo (ii):
Passo (iii):
Como a matriz do lado esquerdo é a identidade, temos a inversa de A do lado direito!
Passo 3
Agora vamos trocar os números diferentes de 0 na matriz inversa por quadradinhos de novo:
Essa matriz está na letra (b).
Resposta
(b)