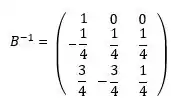Considere as matrizes e .
(b) Determine a inversa de B, a matriz
Passo 1
Para determinar a inversa de uma matriz, devemos escalonar completamente a matriz B junto com a matriz identidade simultaneamente.
Fazendo isso:
Passo (i):
Passo (ii):
Passo (iii):
Passo (iv):
Então, a matriz resultante do lado direito é a matriz inversa da B.
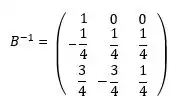
Resposta
Exercícios de Livros Relacionados
Seja A =1 - 1 - 4 1 .Mostraremos no Exemplo 6.6 na página 398 que P = 1 1 - 2 2 e D = 3 0 0 - 1 São tais que A = P D P - 1 .Determine A k , para k =1, 2, 3...
23. Sejam Ax=b um sistema de equações lineares consistente arbitrário e x1 uma solução fixada. Mostre que qualquer solução do sistema pode ser escrita na forma x=x1+x0, em que x0 é a solução de Ax=0.
Simplifique(A C^(- 1))^(- 1) (A C^(- 1)) (A C^(- 1))^(- 1) A D^(- 1)
Use o Teorema 1.4 . 5 para calcular a inversa da matriz A = ([[3,1],[5,2]])
Use o Teorema 1.4 . 5 para calcular a inversa da matriz D = ([[2,0],[0,3]])