P3 – Cálculo Diferencial e Integral 2 – 2021.2 – Profª Cláudia Brunosi Medeiros
Determine o volume do sólido sob o paraboloide acima do plano e dentro do cilindro
Passo 1
Calcular o volume entre a função e o plano dentro de uma região é o mesmo que calcular
Essa região aí para o nosso problema é limitada pelo cilindro que a gente pode pensar como sendo uma repetição ao longo do eixo da circunferência de equação
Passo 2
Como a nossa região de integração é uma circunferência e a gente possui termos de e na nossa integral, vale a pena a gente ir para as coordenadas polares:
Passo 3
Para podermos transformar a nossa integral numa integral que a gente saiba resolver a gente precisa dar uma olhada nos limites de integração. A nossa equação do círculo está um pouco estranha ainda. Isso é porque nosso cilindro não está centrado na origem. Vamos mexer nessa equação para descobrir seu centro
Completamos o quadrado em adicionando em ambos os lados da igualdade
Que é a equação de uma circunferência de raio com centro em . A gente pode fazer um esboço para entender melhor nossos limites
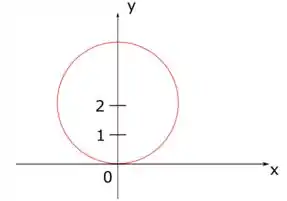
Como pode ser visto na figura acima e lembrando como as coordenadas polares se comportam através da seguinte imagem
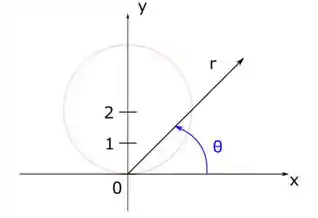
Podemos concluir que para varrer essa região toda, o nosso tem que variar de até ou . O raio que vai ter que virar alguma função diferente aí já que ele vai ter que desenhar esse círculo que a gente representou. Para descobrir seu limite, a gente usa as definições de e na equação do círculo que nos foi dada
Lembrando que nas coordenadas polares temos temos então
Então a nossa região fica compreendida com
Passo 4
Vamos montar a integral em coordenadas polares
Passo 5
Como nossa integral é iterada, podemos resolver isoladamente a integral em primeiro:
Devolvendo esse resultado na nossa integral temos
Para resolver essa integral usamos que
Usando , temos