UFMG, Sem Campus, Cálculo 2, Listas de Exercícios - Lista de Exercícios 5, Questão 1.1b
Encontre outras duas representações em coordenadas polares dos pontos abaixo, uma com e outra com .
b)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede mostrar outras duas representações em coordenadas polares para o ponto abaixo:
Onde uma representação deve ter e outra deve ter .
Mas antes, vamos relembrar um pouco sobre a definição de coordenadas polares?
Bom... As coordenadas polares, são formadas por um sistema bidimensional , em que cada ponto no plano é determinado por uma distância e um ângulo em relação ao ponto fixo de referência.
Na figura abaixo a gente pode ver que um ponto pode ser representado por em coordenadas cartesianas e em em coordenadas polares:
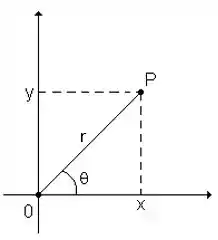
Para encontrar outras duas representações em coordenadas polares desse ponto , podemos usar ângulos equivalentes, adicionando ou subtraindo múltiplos de .
E aí? Vamos partir para o que a gente quer agora??
😉
Passo 2
Vamos fazer primeiro para .
Bom... nesse sentido, vamos inverter o sinal do raio () enquanto mantemos o ângulo () constante.
Uma representação possível com seria escolher o raio como , mantendo o ângulo .
Logo, temos o ponto .
Passo 3
Agora, para .
Nesse caso, podemos manter o raio constante, mas escolher um ângulo equivalente.
Dessa forma, adicionando , obtemos um ângulo de .
Assim, temos o ponto .
Entendeu direitinho? Responde aee ;)
Resposta
e