UFU, Sem Campus, Cálculo 1, Listas de C1 - Profº Rafael Rossato - Integrais com coordenadas polares, Questão 2e
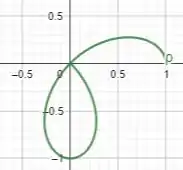
Em cada item desenhe a curva cuja equação é dada em coordenadas polares.
e)
Passo 1
Eaee!!! Belezinha? Seguinte... a questão nos pede para desenhar a seguinte curva cuja equação é dada em coordenadas polares:
Vamos definir o intervalo .
Mas para isso a gente tem que relembrar um pouquinho sobre esse tipo de coordenadas né?
Bom... a gente está acostumado com as coordenadas e . Abaixo segue uma relação mostrando a relação entre os dois tipos de sistema de coordenadas para determinar um ponto :
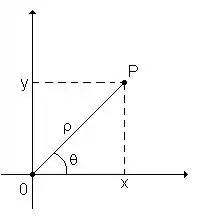
Através dessas informações podemos responder nosso problema!!
No caso do nosso probleminha, vamos atribuir alguns valores a e verificar o resultante. Depois disso basta a gente plotar!!
E aí? Bora lá??
😉
Passo 2
Nesse sentido, atribuindo alguns valores para (em graus), temos:
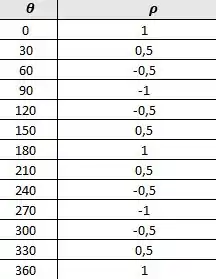
E, convertendo para coordenadas cartesianas, temos, respectivamente:
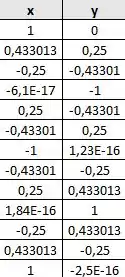
Obs: o ideal é fazermos mais pontos para termos um contorno melhor da nossa figura 😉
Dessa forma, plotando a figura, temos:
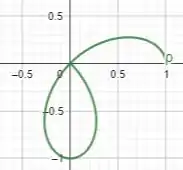
Entendeu direitinho? Responde aee ;)
Resposta
