Determine a área de interseção das figuras e . Faça o gráfico das figuras marcando a área de interseção.
Passo 1
Gaaaalera, falaí! Se liga que para esboçar gráficos polares devemos montar uma tabela , usando aproximações às raízes como e , com ângulos notáveis para que possamos determinar pontos do gráfico e depois traça-se o contorno ligando-os. Assim, considere e . Para o primeiro:

Trace os eixos e e trace retas partindo da origem nos ângulos escolhidos com auxílio de régua e transferidor. Com a régua demarque as distâncias encontradas na direção correspondente e faça o traço, ligando as marcações:
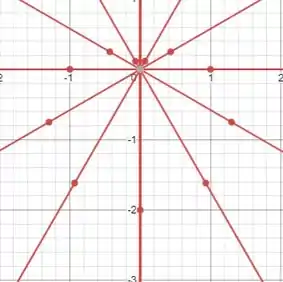
Passo 2
Mantendo as linhas auxiliares vermelhas vamos montar a tabela e traçar seu contorno. Como temos:

Traçando os novos pontos nas respectivas direções angulares, podemos fazer o contorno dessa curva:
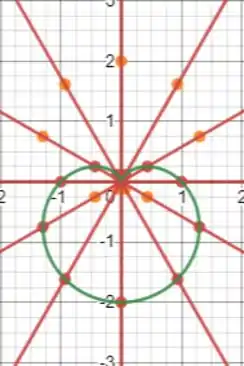
Passo 3
Apagando as linhas auxiliares, a região de interseção entre as curvas é dada por:
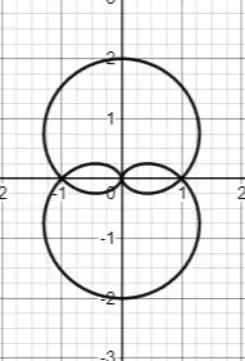
Entre os laços menores das curvas.
Resposta
Ei, a resposta está no passo a passo :)