UFMG, Sem Campus, Cálculo 2, Listas de Exercícios - Lista de Exercícios 5, Questão 1.4c
Identifique a curva encontrando a equação em coordenadas cartesianas para as curvas:
c)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para encontrarmos a equação em coordenadas cartesianas da seguinte equação dada em coordenadas polares:
Para isso, temos que ter em mente as seguintes relações entre os dois tipos de coordenadas:
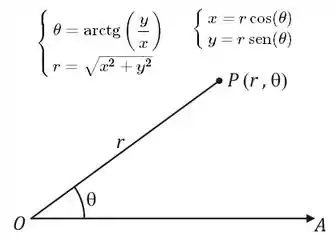
E aí? Bora lá?
😉
Passo 2
Dessa forma, sabemos que:
E
Logo, substituindo na expressão, temos:
Multiplicando os dois lados por , temos:
Passo 3
Sabemos que, pelas relações apresentadas no Passo 1, temos que:
Substituindo na equação do Passo 2, temos:
Completando quadrado para e , temos:
Essa é a equação de uma circunferência de raio com centro no ponto .
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Escreva uma equação polar de uma cônica com o foco na origem e com os dados fornecidos. P a r á b o l a , v é r t i c ee m4 ,3 π 2 á é
A órbita de Marte em torno do Sol é uma elipse com excentricidade 0,093 e semieixo maior 2,28.10 8k m . Encontre uma equação polar da órbita.
O cometa Hale-Bopp, descoberto em 1995 , tem uma órbita elíptica com excentricidade 0,9951 e o comprimento do eixo maior é 356,5A U . Encontre uma equação polar para a órbita desse cometa. Quão perto
A órbita do cometa Halley, visto pela última vez em 1986 e com retorno esperado para 2062 , é uma elipse com excentricidade 0,97 e com um foco no Sol. O comprimento do eixo maior é 36,18A U . [Uma uni
Usar r0 e- 2 πθ ≤ 0 Para escrever os pontos P 1 3 , - 1 e P 2 - 2 ,- 2 em coordenadas polares.