UFMG, Sem Campus, Cálculo 2, Listas de Exercícios - Lista de Exercícios 5, Questão 1.5c
Encontre a equação polar das curvas em coordenadas cartesianas abaixo:
c)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para encontrarmos a equação polar da seguinte curva dada em coordenadas cartesianas:
Para isso, temos que ter em mente as seguintes relações entre os dois tipos de coordenadas:
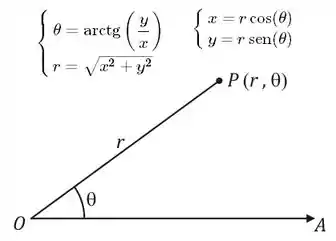
E aí? Bora lá?
😉
Passo 2
Dessa forma, pelas equações mostradas no Passo 1, vemos que:
E que:
Assim, substituindo e , temos:
Colocando o em evidência, temos:
Podemos simplificar o de tal forma que:
Por outro lado, vale lembrar da seguinte identidade trigonométrica:
Portanto, temos:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Escreva uma equação polar de uma cônica com o foco na origem e com os dados fornecidos. P a r á b o l a , v é r t i c ee m4 ,3 π 2 á é
A órbita de Marte em torno do Sol é uma elipse com excentricidade 0,093 e semieixo maior 2,28.10 8k m . Encontre uma equação polar da órbita.
O cometa Hale-Bopp, descoberto em 1995 , tem uma órbita elíptica com excentricidade 0,9951 e o comprimento do eixo maior é 356,5A U . Encontre uma equação polar para a órbita desse cometa. Quão perto
A órbita do cometa Halley, visto pela última vez em 1986 e com retorno esperado para 2062 , é uma elipse com excentricidade 0,97 e com um foco no Sol. O comprimento do eixo maior é 36,18A U . [Uma uni
Usar r0 e- 2 πθ ≤ 0 Para escrever os pontos P 1 3 , - 1 e P 2 - 2 ,- 2 em coordenadas polares.