Calcule .
Passo 1
Vamos resolver a integração em primeiro. Como a função a ser integrada não depende de temos
Passo 2
Que integral horrorosa para resolvermos hein?! Mas calma lá... com esse monte de e a gente começa a suspeitar que podemos usar as coordenadas polares. Dá uma olhada nos limites de integração:
O varia entre -2 e 2 e o varia entre as funções
Se elevarmos as duas funções ao quadrado, temos
Que é exatamente a equação de um círculo de raio 2. Olha só como a nossa região de integração fica
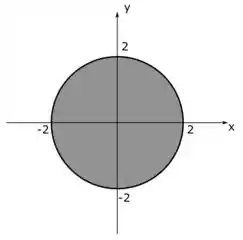
Logo, ir para as coordenadas polares vai ser uma boa ideia. Essa região pode ser descrita se usarmos
Onde é o raio do círculo e é o ângulo que cresce a partir da parte positiva do eixo no sentido anti-horário. Essas variáveis estão definidas nos intervalos
Passo 3
Para podermos mudar as coordenadas na nossa integral, precisamos saber como aqueles mudam nas coordenadas polares. Toda vez que a gente sai das coordenadas e para as coordenadas e teremos
Onde o é o módulo do determinante do Jacobiano. Nas coordenadas polares é conhecido que
Agora temos tudo em mãos para reescrevermos a nossa integral. Ficamos com
A única coisa que nos resta é como essa função vai ficar quando eu usar
Mas relaxa, você pode usar esses valores de e de na integral sem problema nenhum mas é mais fácil você lembrar da equação do círculo:
E esses termos aparecem direto na nossa integral. Escrevemos então
Passo 4
Viu que nossa integral monstruosa virou essa integral mais simpática aqui?
Essa é uma integral iterada e a gente pode resolvê-la primeiro resolvendo a integral em separadamente
Passo 5
Agora podemos resolver a integral em