Calcule onde
E é a curva percorrida de a .
Passo 1
Bom, já deu pra ver que calcular isso aí direto pela definição não é muito fácil né. Certo, mas esse rotacional vai dar zero, para facilitar nossa vida.
Mas presta atenção em uma coisa: temos uma indeterminação em nos termos com fração, o que nos dificulta usar os conceitos de campos conservativos. Então, vamos dividir esse campo em duas partes:
A primeira não dá problema nenhum para a gente, mas segunda sim. Temos;
Passo 2
Vamos começar calculando . Antes de tudo, calculamos o rotacional:
Como está definido em todo o e seu rotacional deu zero, podemos dizer que o campo é conservativo.
Passo 3
Então, vamos encontrar uma função potencial para esse campo, temos:
Onde é o operador de derivadas parciais:
Temos então o seguinte:
Vamos agora igualar termo a termo esses vetores.
Comparando as equações, vemos que:
O que nos dá
Passo 4
Bom, se o campo é conservativo, podemos calcular a integral de linha usando sua função potencial, não é?
Pela definição de função potencial, nós sabemos do seguinte:
Ou seja, em um campo conservativo, a integral de linha sobre a curva é igual ao valor da sua função potencial no ponto final menos o valor no ponto inicial.
Agora é só calcular e .
Logo,
Passo 5
Ok, agora precisamos da integral de . Vamos fazer o seguinte: fechamos uma região que não contenha o ponto (que é o problemático) e aplicamos Green, ok?
Para a gente ter uma ideia, a curva é essa aqui:
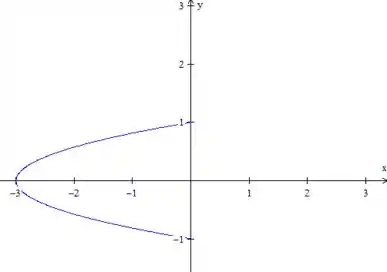
Como o campo tem o termo no denominador, vamos isolar a origem com a elipse
Na verdade, com o arco dessa elipse que vai de até . Assim, a curva toda gira no sentido anti-horário.
Aplicando Green, temos então:
Onde e são as componentes do campo e é o arco da elipse.
Passo 6
Vamos calcular agora esse rotacional aí:
Isso nos dá:
Ótimo, então temos:
Passo 7
Beleza, para terminar a questão falta só a integral no arco de elipse então. Vamos começar parametrizando ela em coordenadas elipticas:
Como o sentido dela é horário (de até , temos de a .
Agora, derivamos essa parametrização:
Escrevendo o campo nas variáveis da parametrização, temos:
Então, podemos levar tudo para a fórmula:
Passo 8
Agora vamos juntar tudo o que sabemos:
Portanto: