Calcule o trabalho do campo
ao longo da curva parametrizada por com
Passo 1
Primeira coisa que a gente vai fazer aqui é calcular esse rotacional, que é feito desse jeito:
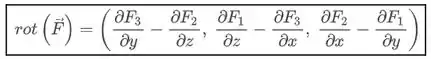
Opa, que maravilha. Uma vez que nosso rotacional é nulo e o campo não tem singularidade nenhuma, a gente sabe que existe uma função potencial para esse . Vamos então buscar essa função .
Passo 2
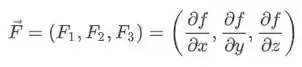
Para descobrirmos a função potencial , basta resolvermos então as integrais.
Resolvendo então primeiro 1):
Resolvendo agora 2):
E por último, mas não menos importante, resolvemos 3):
Com isso concluímos que a função potencial é:
Passo 3
Esse é o momento em que aplicamos os pontos iniciais e finais:
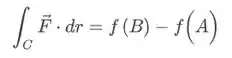
Vamos ver então quais são os pontos substituindo nossa parametrização dada no enunciado pelos extremos.
Teremos então:
Lembrando que