Seja o campo
- Determine as constantes reais , e de modo que
- Para as constantes determinadas no item (a), calcule onde
Orientada de modo que o ponto inicial seja .
Passo 1
Letra a)
Precisamos encontrar as constantes , e que façam o rotacional desse campo ser zero. Ou seja:
Nós podemos calcular no braço o rotacional desse campo enorme:
E igualar ele a zero. Mas vamos pensar de forma diferente, para poupar trabalho. Pensa na defininção de campo conservativo. É o campo que tem rotacional igual a zero e que possui uma função potencial tal que
Onde é o operador de derivadas parciais:
Nós podemos resolver o problema por aí. E isso ainda vai ser útil na letra b) da questão, você vai ver! Temos então o seguinte:
Passo 2
Vamos agora igualar termo a termo esses vetores.
Comparando as equações, vemos que:
Passo 3
Letra b)
Como o campo é conservativo e a integral independe do caminho, vamos usar a função potencial para calcular a letra b) da questão:
Nós já sabemos, pela questão, que o ponto inicial é , mas e o final? Vamos tirar isso das outras informações que o enunciado deu:
Essa é a definição da curva onde é feita a integral de linha. Temos uma esfera e os planos , e . Graficamente, é isso aqui:
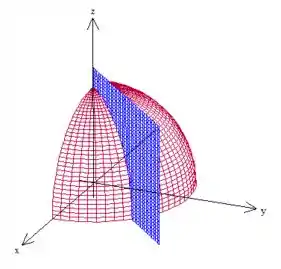
A curva é dada pela interseção entre essa parte da esfera e o plano azul, um arco de circunferência, como podemos ver. Como o ponto inicial é o , é o lá de cima, que fica no eixo . O ponto final pertence ao plano , logo, o sentido da curva é “descendo” no arco. Viu?
Vamos achar ele então agora!
Substituindo na equação da esfera, temos
Agora vamos com calma, isso é a projeção da nossa curva no plano , como se estivéssemos olhando a curva de lado. Por isso que é uma elipse, não um circunferência.
Como sabemos que o nosso ponto pertence ao plano , sabemos que , então vamos substituir isso na equação que acabamos de achar para encontrar o do nosso ponto:
Ótimo, agora só falta o , né? Já sabemo que o é zero. Como o plano é , temos uma simetria, já dá pra sacar que:
Mas se você não percebeu isso, não temo problema, podemos tirar a coordenada da própria equação da esfera, substituindo e que já temos nela:
Então, temos que o ponto final é o seguinte:
Passo 4
Agora vamos calcular isso aí:
Onde é dada por:
Logo: