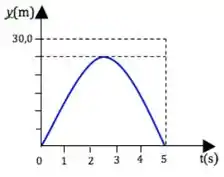
Uma bola é lançada verticalmente para cima a partir da superfície de um certo planeta. O gráfico da sua altura em função do tempo é mostrado no gráfico abaixo, cuja escala vertical é definida por . O módulo da aceleração em queda livre no planeta em é:
Passo 1
Parece complicado né? Mas calma, vem comigo que você entende. Tá vendo aquele flutuando ali? A curva nem alcança essa altura, então porque ele tá ali? Dá uma olhada:
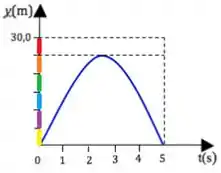
Tá vendo os tracinhos coloridos? Espero que sim se não a página está em preto e branco! De qualquer forma, eles tão ali pra gente ficar atento que são todos iguais! Então a altura de pode ser dividida em , de forma que cada tracinho tenha de tamanho, beleza? Se a nossa querida curva tem tracinhos de altura máxima então a gente vai esquecer esse e vamos considerar a altura máxima como tendo o valor de .
Passo 2
Como o gráfico descreve um lançamento vertical, vamos separar dois pontos importantes da nossa curva: o ponto de altura máxima e o ponto de retorno da bola. A gente vai fazer isso porque nesses pontos o gráfico conta tudo pra gente: o tempo e a posição. Então partiu, vamos pras contas. No ponto de altura máxima:
Dá uma olhada no gráfico: A altura máxima a gente já sabe, mas e o tempo que demora pra alcançar essa altura, qual é? Bem, no gráfico, a gente vê que é metade do tempo total, então:
Eita, tem duas incógnitas ai! E agora? Relaxa, falta ver o ponto de retorno da bolinha. Nesse ponto, a altura final e inicial são a mesma! E bem, o tempo que demora pra bola voltar é o tempo total, certo? Então, partiu:
Passo 3
Pera lá, duas equações e duas incógnitas? Isso tem cara de sistema de equações não tem? Então resolvendo o sistema, a gente acha a gravidade: