USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 10d
Um objeto é lançado verticalmente, em com uma velocidade de para cima, de uma janela situada a do solo.
d) Determine a distância total percorrida para o intervalo e a altura máxima que o objeto atinge.
Passo 1
Fala aí pessoal, tudo tranquilo?
Nessa questão temos um objeto que está situado em uma janela a do solo. Ou seja:
Ele é lançado para cima com uma velocidade inicial de . Como o enunciado nos fala que o eixo de referência está orientado para cima, escrevemos que:
Perfeito!
Como o objeto descreve um movimento retilíneo uniformemente variado (MRUV), com a gravidade atuando como desaceleração, vimos que o seu deslocamento é expresso por:
Precisamos determinar a distância total percorrida pelo objeto e a altura máxima atingida por dele.
Mas, o que acontece quando a altura é máxima??
A velocidade do objeto se anula! Então, como também vimos que, por se tratar de um MRUV, vale:
Vamos encontrar o instante em que a altura é máxima para a partir disso calculá-la efetivamente.
Vem com a gente 😊
Passo 2
Vimos que a altura é máxima quando a velocidade se anula. Assim:
Então, para o objeto deve estar atingindo a altura máxima. Logo:
Logo:
Essa é a altura máxima atingida pelo objeto.
Passo 3
Já para calcular a distância total percorrida pelo objeto não basta apenas calcularmos o , pois ele vê apenas a diferença entre a altura que o objeto se encontra em um instante e a altura inicial.
Pra calcular a distância total podemos usar o artifício do gráfico, como:
O gráfico é dado por:
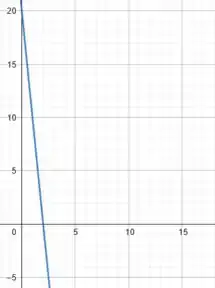
Pra calcular a distância total percorrida podemos encontrar a área abaixo da curva azul no intervalo , sem considerar áreas “positivas” e “negativas”. Assim, estamos tomando cada distância percorrida em módulo.
Como trata-se de um triângulo, se estamos em um tempo , vale que a área desse triângulo:
onde:
é a altura do triângulo.
Assim:
Então:
E é isso gente!!
Muito obrigado pela atenção e até a próxima 😉
Resposta
(altura máxima)