UFSCAR, Sem Campus, Física 1, AV1 - 2021.1 - Prof° Raphael Santarelli, Questão 4a
Uma partícula se move em uma trajetória circular horizontal no plano , com velocidade escalar constante. No instante , a partícula possui velocidade e aceleração no sentido positivo de . No instante , a partícula possui velocidade e aceleração no sentido positivo de . Considere a diferença é menor que um período de rotação.
Faça um desenho da trajetória circular no plano , e identifique o sentido de rotação e os pontos e .
Passo 1
Oiie, tudo certinho?
Temos aqui uma partícula se movendo em uma trajetória circular sobre o plano , o enunciado nos dá algumas informações sobre instantes da trajetória, como por exemplo, nos indica que no instante , a velocidade da partícula é tal que
da mesma forma, temos que em , a velocidade é tal que
O enunciado também nos dá informações sobre a direção da aceleração nestes dois instantes, no primeiro instante a aceleração está no sentido positivo de , e no segundo instante, está no sentido positivo de . Por último, nos é afirmado que , em que é um período de rotação! Belezinha?
Esta alternativa nos pede para fazermos um desenho da trajetória circular usando as informações dadas acima! Note, que é uma questão de analisar a escolha de referencial! Vai ser bem rápido! Bora lá!
Passo 2
Primeiro, vamos escolher um referencial com origem no centro de nossa trajetória circular
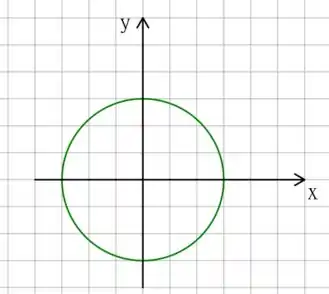
vamos colocar agora o primeiro instante de tempo relevante e o vetor velocidade relacionado! Temos que em , o vetor velocidade é , ou seja, o nosso vetor é
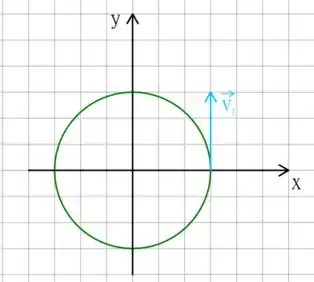
Em um instante posterior , temos que o vetor é que pode ser representado como
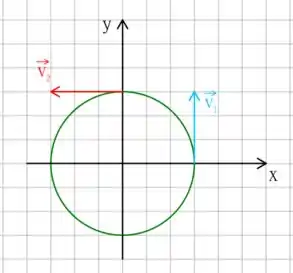
Note que o sentido de rotação é anti-horário! Portanto, apenas por completeza, podemos terminar o desenho como
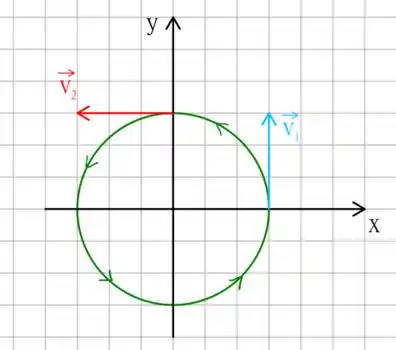
Essa foi a primeira alternativa! Te vejo na próxima! Até jajá!
Resposta
Ao longo do passo 2.