Durante um experimento de física experimental I duas esferas e de massas, foram abandonadas de uma mesma altura . Podemos então afirmar que a relação entre os tempos de queda das duas esferas é igual a:

(a)

(b)

(c)

(d)

(e)

Fala aí!!!

Se as bolinhas foram abandonadas de uma altura , então estamos falando de um movimento de queda livre. Ou seja, a velocidade inicial delas é zero.

Com isso temos:

E

Para as duas bolinhas.

Vamos desenhar o que temos:

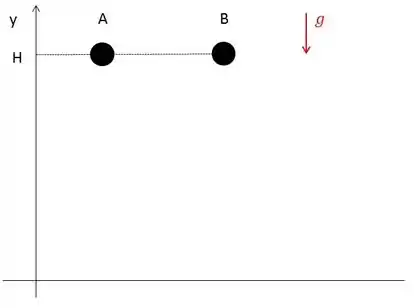
Já coloquei a aceleração da gravidade ali. Notem que, como ela aponta pra baixo, vamos ter:

Assim, ambas as bolinhas descrevem um MUV.

E a posição varia no tempo de acordo com:

A posição final é , pois elas vão chegar no chão.

Então, para a bolinha A:

Então:

Para a bolinha B, vai ser a mesma coisa, já que elas têm todas as características, que importam, iguais. A equação que dá a posição em função do tempo independe da massa.

O tempo de descida é igual para ambas, desconsiderano o atrito com o ar. Não importa a massa.