Um corpo de massa é abandonado do topo de um prédio de altura distante do solo . Qual deverá ser o valor das velocidades do corpo, respectivamente a do solo e imediatamente quando toca o solo?
Desconsidere os atritos e considere .
(a) s e ;
(b) e ;
(c) e ;
(d) e ;
(e) e
Passo 1
Fala aí!!!
Eles estavam em cima de um prédio quando deixaram a bolinha cair, então a altura inicial é:
Quando ele fala pra gente que um corpo é abandonado, quer dizer que ele saiu do repouso, ou seja a velocidade inicial é zero.
Desenhando o que ele fala pra gente, temos:
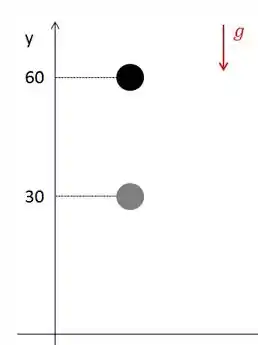
Queremos a velocidade quando a posição é e quando ele chega ao solo, ou seja quando .
Beleza!
Como relacionamos essas coisa???
Passo 2
Vimos que temos aceleração da gravidade, e ela é um valor constante, então estamos vendo um movimento uniformemente variado.
Notando que, como a gravidade aponta pra baixo em relação ao eixo y, temos:
E as equações do MUV que relacionam a posição e tempo, e a velocidade e o tempo são:
E
Maravilha!!
Passo 3
Pra gente achar a velocidade quando a altura é :
A altura inicial é , a velocidade inicial é 0, porque ele sai do repouso, e a aceleração é Substituindo isso tudo:
Resolvendo isso:
Beleza, aqui descobrimos o tempo que a bolinha demorou pra chegar na posição Mas o que ele quer é a velocidade quando ela tá nessa posição!
Bem, depois de passar ela vai estar em , então para descobrirmos a velocidade correspondente:
Então
O valor tá com o menos na frente porque o sentido da velocidade é para baixo em relação ao nosso eixo y de referência.
Uhuul!!
Já temos metade da resposta!
Passo 4
Pra gente achar a velocidade quando a altura é :
A altura inicial é , a velocidade inicial é 0, porque ele sai do repouso, e a aceleração é Igualzinho no caso anterior.
Substituindo isso tudo:
Resolvendo isso:
Beleza, aqui descobrimos o tempo que a bolinha demorou pra chegar chão.
Bem, depois de passar ela vai estar em , então para descobrirmos a velocidade correspondente:
Então
Da mesma forma que o anterior, o valor tá com o menos na frente porque o sentido da velocidade é para baixo em relação ao nosso eixo y de referência.
Maravilha!!!

Resposta
Alternativa (c)