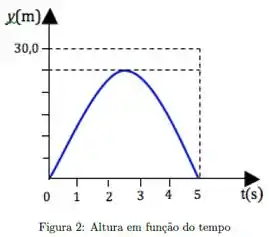
Uma bola é lançada verticalmente para cima a partir da superfície de um certo planeta. O gráfico da sua altura em função do tempo é mostrado no gráfico 2, cuja escala vertical é definida por . O módulo da aceleração em queda livre no planeta é:
(a)
(b)
(c)
(d)
(e)
Passo 1
Em um lançamento vertical para cima, o tempo de subida é igual ao tempo de descida. Então, pelo gráfico a gente descobre que a bola alcança a altura máxima em .
Além disso, o enunciado diz que a sexta marcação do eixo é (cada marcação representa ). A altura máxima da bola é na quinta marcação, portanto:
Agora, vamos usar as equações de movimento uniformemente variado para achar a aceleração da gravidade no planeta.
Passo 2
Quando o corpo atinge a , sua velocidade é zero. Então, podemos considerar o movimento a partir do instante como uma queda livre.
Podemos utilizar a seguinte expressão:
Usando o referencial do gráfico, a posição inicial será , a posição final será , a aceleração será e a velocidade inicial já vimos que também é zero:
Agora, vamos substituir os valores de e :
Porque, achamos um valor negativo?
Porque nosso referencial aponta para cima, logo a gravidade está no sentido contrário (como já era esperado).
Achamos que o módulo da aceleração é:
Ficamos com a alternativa (a).
Resposta
Letra (a)