Q - Um garoto observa um gafanhoto quando este dá um salto vertical de metros. As pernas deste gafanhoto têm de comprimento. Para saltar o gafanhoto desdobra as suas pernas rapidamente e consegue realizar saltos enormes quando comparados ao seu tamanho. Despreze o atrito do ar, e adote .
Qual a aceleração média alcançada pelo gafanhoto no intervalo de tempo em que ele desdobra as pernas?
Quanto tempo dura este salto do instante em que ele abandona o chão até o instante em que ele volta à posição inicial?
Faça o gráfico de do momento em que o gafanhoto começa o movimento para saltar até o seu retorno ao solo.
Passo 1
Vem comigo que a gente detona essa questão!
Analisando a situação descrita pelo enunciado, podemos tirar algumas seguintes informações.
O deslocamento do gafanhoto do chão até o ponto mais auto de sua trajetória é .
A altura que ele alcança antes de sair do chão quando está com as pernas esticadas é .
E a distância que ele percorre quando sai do chão é .
Disso podemos tirar que:
Para achar a aceleração pedida em que o gafanhoto tem no tempo em que ele desloca as pernas, temos que analisar a velocidade usando a equação de Torricelli enquanto ele estica as pernas e depois no movimento dele até o ponto mais alto da sua trajetória.
Vamos usar essa equação, pois o enunciado não nos falou nada sobre o tempo nesses processos.
Para o item , temos que lembrar que o tempo total do salto equivale ao tempo de subida mais o tempo de descida, mas como eles são iguais podemos encontrar apenas um deles e multiplicar por dois.
Mas temos que lembrar que esse tempo é a partir do momento em que ele sai do chão.
E vamos usar a equação da velocidade da cinemática dada por:
Onde é a velocidade no ponto mais alto e a velocidade com que ele deixa o chão.
Para montar o gráfico de temos que usar a mesma equação acima só que com as informações que conseguimos.
Passo 2
Vamos começar com o item .
Primeiro vamos analisar o movimento na parte em que o gafanhoto está esticando as pernas. Usando a equação de Torricelli, temos:
Substituindo para o que temos, ficamos com:
Agora o movimento que temos a partir do momento que ele sai do chão, vamos usar o índice , para não confundir nossa cabeça, temos:
Só que agora, a velocidade final , a velocidade inicial é igual a velocidade final que o gafanhoto atinge antes de sair do chão e e , assim temos que:
Usando o que sabemos sobre , temos:
Substituindo os valores que conhecemos, temos:
Item feito com sucesso!
Passo 3
Agora vamos para o item .
Usando a equação da velocidade para a parte do movimento que ele deixa o chão temos:
Esse é o tempo de subida, o tempo total é dado por:
Substituindo com os valores que conhecemos, temos:
Então temos que:
Mais um item finalizado!
Passo 4
Agora vamos atrás do gráfico pedido em .
A equação da velocidade para a primeira parte do movimento é dada por:
Onde e , assim:
Mas temos que saber o intervalo de tempo que essa parte dura, para isso vamos usar a equação da posição, temos:
Substituindo os valores que conhecemos, temos:
Então em a velocidade varia da seguinte forma:
A equação para a segunda parte do movimento é dada por:
Onde temos que:
Assim em , temos que:
Sabendo de tudo isso o gráfico fica da seguinte forma:
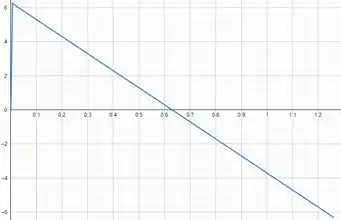
E com isso a nossa questão está terminada!
Resposta