UFMG – Fundamentos de Mecânica – P1 – Questão P1.3
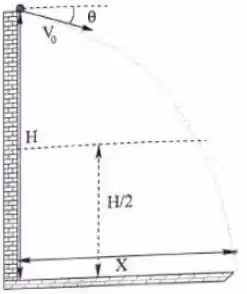
Uma bolinha de massa m é lançada de um muro, fazendo um ângulo com a horizontal para baixo, saindo do muro de uma altura H a partir do solo. Mede-se que a bolinha leva um tempo T para atingir o solo, a partir do instante que sai do muro. Dê suas respostas em função de e .
3) Calcule o tempo que a bolinha gasta para passar pela metade da altura do muro
Passo 1
Oi, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Queremos determinar o tempo no qual a bolinha passa pela altura .
Relembrando das equações de movimento para a componente (isso porque queremos saber , que está na direção vertical)
E ideia para resolver questões de cinemática é comparar os dados que temos com as equações
Isso sem esquecer que a velocidade inicial pode ser decomposta em componente vertical e horizontal
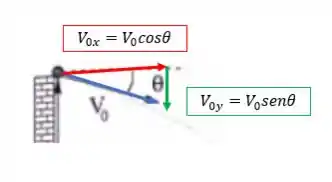
tranquilo até aqui?
Temos e e queremos saber , então através das equações de movimento vamos encontrar essa altura!
Vamos lá?
Passo 2
A bolinha saiu de uma posição inicial com uma velocidade inicial de . E queremos determinar o tempo que ela leva para atingir a posição . Ou seja, é interessante usar uma equação que relaciona posição e tempo, não é verdade?
E essa é a primeira equação daquele monte de equações do passo anterior!
Essa é a equação horária do movimento: ela relaciona a posição que o corpo vai passar com o instante que isso vai acontecer!
Agora é só substituir os valores!
Passo 3
Os dados que temos são
E queremos saber ! A equação é
Substituindo os valores temos
Reorganizando os termos:
E multiplicando tudo por :
Temos uma equação de segunda ordem!
E como resolvemos isso? Pela fórmula de bhaskara!
Passo 4
Nossa equação é:
Os coeficientes são:
Agora é só substituir na bhaskara:
E não tem muito mais que podemos fazer! Temos duas raízes (vamos descartar a negativa, pois não existe tempo negativo na física) e podemos escrever um pouco mais simples essa expressão
E é isso! Esse é o tempo que a bolinha leva para chegar na metade da altura do prédio!
Beleza?
Espero ter ajudado!