USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 10c
Um objeto é lançado verticalmente, em com uma velocidade de para cima, de uma janela situada a do solo.
c) Calcule o deslocamento do objeto para os intervalos e ;
Passo 1
Ooi galerinha, tudo beleza?
Nessa questão temos um objeto que está situado em uma janela a do solo. Ou seja:
Ele é lançado para cima com uma velocidade inicial de . Como o enunciado nos fala que o eixo de referência está orientado para cima, escrevemos que:
Perfeito!
Como o objeto deve descrever um movimento retilíneo uniformemente variado (MRUV), o seu deslocamento deve seguir a expressão:
onde é a distância inicial, a velocidade inicial e a aceleração do objeto.
Sabendo disso, podemos calcular o deslocamento do objeto nos intervalos de a e de a.
Vamo nessa!
Passo 2
Pra começar, temos a expressão:
Vamos identificar quem é cada termo:
é o deslocamento inicial, ou seja, altura inicial no contexto do nosso problema. Então:
Já , que é a velocidade inicial, temos:
E, a aceleração é na verdade uma desaceleração que vem da gravidade. Então:
Assim, podemos escrever:
Logo, o deslocamento será dado por:
Essa expressão vale tanto para como pra .
Passo 3
Uma outa forma de resolver esse exercício, que dá um pouquinho mais de trabalho, é calcular o deslocamento do objeto através da área do gráfico .
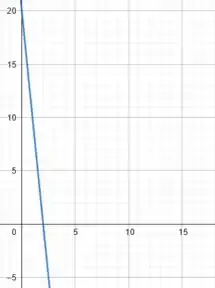
Nesse caso teríamos que considerar como áreas positivas aquelas acima do eixo e áreas negativas aquelas abaixo do eixo .
Mas, usando a nossa equação horária do MRUV conseguimos a resposta bem mais rápido 😊
Então é isso pessoal, até a próxima!