UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 4d.
3- Desenhe as curvas de nível das funções de duas variáveis a seguir para os valores de dados:
d) ;
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Para essa questão vamos ter que calcular as curvas de níveis da função . Ok, mas o que são curvas de níveis?
Curvas de níveis de uma função são obtidas a partir do corte na função a uma altura do plano , formando uma curva correspondente à curva de nível na altura .
Algo muito parecido com desenhos topográficos em Geografia.
Inicialmente temos uma função tridimensional, porém quando tiramos a curva de nível, obtemos uma função bidimensional, já que a variável corresponde à altura.
Com isso podemos iniciar nossos cálculos, substituindo por , temos
Isolando em um lado temos
O próximo passo é substituir pelos valores que foi solicitado.
Passo 2
Observe que está em módulo, logo deve ser . Ou seja, .
Para o nível , a função que representa a curva de nível é
Essa função não é tão intuitiva de se imaginar o gráfico, então podemos usar o método da tabelinha para encontrar pontos que contém a função, estimando valores para , por exemplo
Com este método, obtemos os pontos , , , , , e .
Vamos guardar estes pontos para plotarmos mais tarde.
Passo 3
Para o nível , a função que representa a curva de nível é
Obtendo alguns pontos da função pelo método da tabelinha.
Os pontos que obtemos, foram , , , e .
Para o nível , a função que representa a curva de nível é
Obtendo alguns pontos da função pelo método da tabelinha.
Para este nível, obtemos os pontos , , , , e .
Passo 4
Plotando os pontos que encontramos no plano
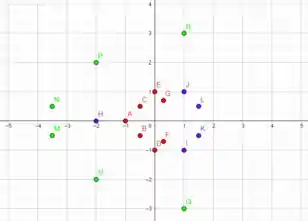
Ligando os pontos do mesmo nível, podemos esboçar as curvas.
Caso alguma curva não esteja tão clara, podemos estimar mais pontos no método da tabela.
As curvas de níveis para , e , temos
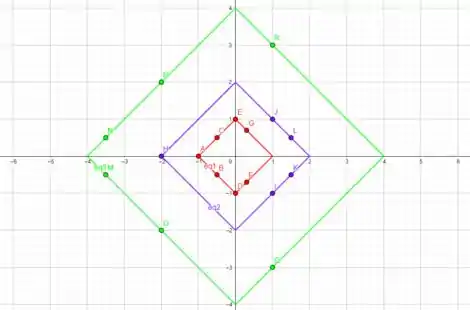
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
Para ,
Para ,
Para ,