James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, São Paulo: CENGAGE learning, 2010, pp. 848, exercício 101e
(Cap 14.3 – Ex 101e) Seja
(e) O resultado da parte (d) contradiz o Teorema de Clairaut? Use os gráficos de e para ilustrar sua resposta.
Passo 1
E ai meus queridos? Tudo certinho?
Então vem comigo que no caminho eu explicooo
O teorema de Clairaut nos diz o seguinte: Suponha que seja definida em uma bola aberta que contenha o ponto . Se as funções e são continua em D, então:
Mas no item anterior, vimos que e . Portanto, não atende ao Teorema de Clairaut.
– Gráfico de
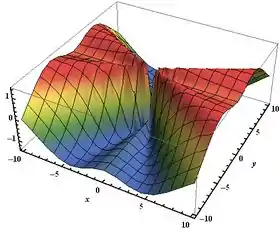
Passo 2
– Gráfico de
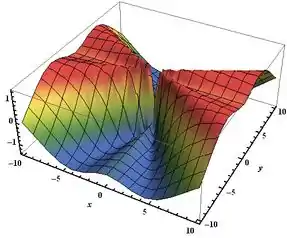
Resposta
Como podemos perceber nos gráficos, há uma descontinuidade em , de modo que não podemos aplicar o Teorema de Clairaut.
Exercícios de Livros Relacionados
Desenhe as curvas de nível e esboce o gráfico. f (x , y) = 4 x^2 + y ² ²
Utilize um computador para traçar o gráfico da função usando vários domínios e pontos de vista. Imprima a que, em sua opinião, oferece a melhor visão. Se seu programa também produz curvas de nível, tr
Esboce o gráfico da função. f x , y = 4 x 2 + y 2
Utilize um computador para traçar o gráfico da função, usando vários pontos de vista e tamanhos de janela. Comente o comportamento da função no limite. O que acontece quando x e y se tornam muito gran
Faça uma correspondência entre a função (a) e seu gráfico (indicado por A-F na página 828), (b) e seus mapas de contorno (indicado por I-VI). Justifique sua escolha. z = x - y 1 + x 2 + y 2