UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 2e.
Esboce o gráfico das funções a seguir:
e)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Para essa questão, foi solicitado que esbocemos um gráfico de , mas você acha que podemos fazer isso? 🤔
Esboçar um gráfico é traçar, de uma forma mais material, a imagem da função.
Uma função está contida em 3 dimensões, ou seja, dependendo de um determinado ponto em e um determinado ponto em , vamos ter uma imagem em , com isso, podemos afirmar que na verdade .
Podemos comparar com uma lei muito famosa, a chamada 3° Lei de Newton ou lei da Ação e Reação. Essa lei da natureza diz que para cada ação, há uma consequência, por exemplo, quando éramos pequenos, tínhamos que comer tudo em uma refeição, caso contrário nossas mães nos botavam de castigo, não é?
Então, nossas ações são nossas variáveis e , no caso, não comer as verduras e legumes. Quando isso acontece, temos uma reação, ou seja, nossa variável ou , que no caso foi nossas mães pôr a gente de castigo.
Entendeu? Para cada valor de e , vamos ter um (para cada ação, vamos ter uma reação)!
Passo 2
Na prática, funciona da seguinte maneira:
Temos a função que vamos esboçar o gráfico
O próximo passo é analisarmos o que esperamos de como será o gráfico.
Neste caso, como você acha que ele vai ser? Plano, ondulado, inclinado, curvo...?
Vemos que independe de , já que não importa o valor de , se for constante, a função terá a mesma imagem.
Uma ótima forma de calcular uma curva, é fazer uma tabelinha determinando valores às variáveis e calculando a imagem resultante.
Como neste caso a função não depende , podemos definir o plano e calcular os pontos no plano .
Se , vamos plotar os pontos , , , e que acabamos de calcular no plano
Passo 3
A próxima etapa é unir os pontos, formando uma curva.
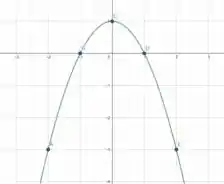
Porém temos um problema, este gráfico está em duas dimensões! Como vamos transforma-lo em três dimensões?
Foi digito anteriormente que, independente de , o valor da função será igual se for constante ou seja durante todo o domínio de teremos sempre a mesma imagem.
Logo em três dimensões a função terá a seguinte estética.
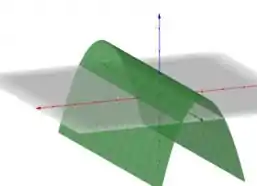
Este é nosso gráfico ! Fazendo um corte perpendicular a em qualquer ponto, teremos sempre o mesmo desenho.
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
Gráfico no último passo.