UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 2b.
Esboce o gráfico das funções a seguir:
b)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Para essa questão, foi solicitado que esbocemos um gráfico de , mas você acha que podemos fazer isso? 🤔
Esboçar um gráfico é traçar, de uma forma mais material, a imagem da função.
Uma função está contida em 3 dimensões, ou seja, dependendo de um determinado ponto em e um determinado ponto em , vamos ter uma imagem em , com isso, podemos afirmar que na verdade .
Podemos comparar com uma lei muito famosa, a chamada 3° Lei de Newton ou lei da Ação e Reação. Essa lei da natureza diz que para cada ação, há uma consequência, por exemplo, se levantarmos tarde e deixar a cama desarrumada, nossas mães vão ficar bravas sendo capaz até de nos botar de castigo, não é?
Então, nossas ações são nossas variáveis e , no caso, levantar depois do horário e não arrumar a cama. Quando isso acontece, temos uma reação, ou seja, nossa variável ou , que no caso foi nossas mães ficarem bravas e pôr a gente de castigo.
Entendeu? Para cada valor de e , vamos ter um (para cada ação, vamos ter uma reação)!
Passo 2
Na prática, funciona da seguinte maneira:
Temos a função que vamos esboçar o gráfico
O próximo passo é analisarmos o que esperamos de como será o gráfico.
Neste caso, como você acha que ele vai ser? Plano, ondulado, inclinado, curvo...?
Vemos que a função não possui no lado direito da equação.
Nesse caso então, seguindo a analogia do que dissemos agora pouco, temos apenas uma ação.
Se a função não possui , não importa se é indepentente de a imagem de vai ser a mesma, o que vai influenciar é o valor de .
Diante disso, podemos considerar inicialmente como .
Tá, mas e o bendito gráfico?
Passo 3
Uma maneira bastante intuitiva de elaborar um gráfico, é começar fazendo uma tabela atribuindo valor às variáveis para ver qual será a imagem formada, por exemplo
Substituímos o valor atribuído a em e o resultado é a imagem que buscamos.
Passando esses pontos para um plano cartesiano , onde e .
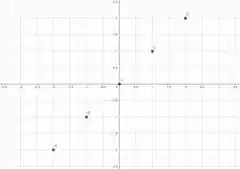
Estamos trabalhando em duas dimensões e como foi dito no início, está em 3 dimensões.
Ou seja, temos que voltar de para .
Sabemos que independe, então como vamos fazer com a projeção do eixo ?
Passo 4
No plano que plotamos os pontos anteriormente aparece como se estivéssemos na origem de , ou seja, , quando vamos para , os pontos mudam?
Como não depende de , a resposta é não, os pontos não mudam, assim como em ... ou seja, para o eixo os pontos seguir sendo plotados na mesma coordenada em e em .
O que é uma sequência contínua de pontos?
Uma reta!
Logo, em 3 dimensões, os pontos vão se transformar em retas.
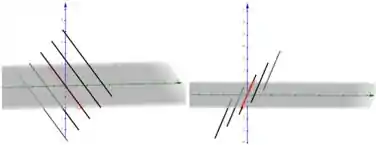
Unindo as retas, vamos ter um plano que será o resultado final do gráfico de !
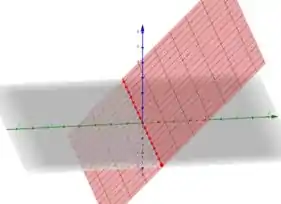
Assim conseguimos plotar um gráfico em 3 dimensões
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
Gráfico no passo 4.