UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 7c.
7- Dada a função , pede-se:
c) Um esboço do gráfico da função.
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Para resolver essa questão, no enunciado foi dada uma função e neste item foi pedido para esboçar o gráfico de .
Nos itens anteriores, encontramos a equação que descreve as curvas de níveis da função
Que são circunferências de raio e as curvas de níveis para , e
Vemos também que as curvas de níveis são circunferências que quanto maior o nível, menor o raio.
Uma maneira de construir um gráfico tridimensional é determinar algumas curvas de níveis e cortes para facilitar a imaginação de como deve ser o gráfico.
Passo 2
Temos as curvas de níveis para , e . Plotando-as em 3D no nível determinado, temos
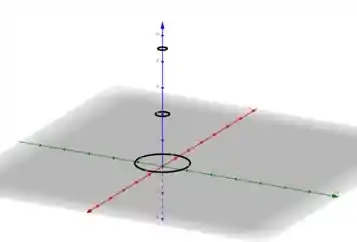
Só com isso ainda não fica tão claro de como o gráfico se comporta.
Uma maneira muito interessante é fazer alguns cortes, por exemplo, como deve ser o corte do plano com a função ? E do plano ?
Pra isso, a gente substitui em e encontramos uma função bidimensional, depois o mesmo para , veja só
Passo 3
Plotando esses cortes em 3D junto com as curvas de níveis que tínhamos encontrado, temos
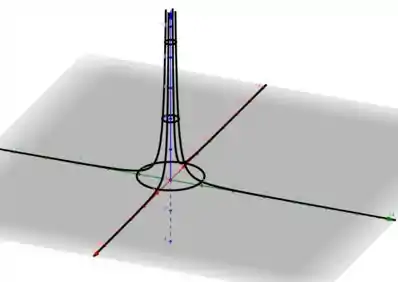
Agora ficou mais visível, não é?
Ligando as curvas que encontramos, vamos ter um sólido que será nosso gráfico de .
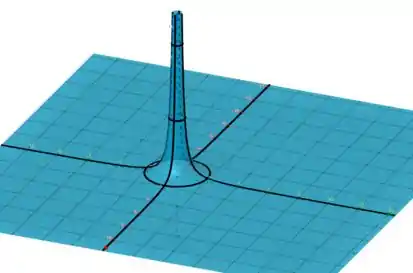
Caso os cortes e as curvas de níveis não estejam tão claros, podemos usar o método da tabelinha, que consiste em determinar valores para a variável da função e encontrar sua imagem no plano, assim formando um ponto, e sabemos que com vários pontos, temos uma curva.
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí