UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 6.
Se é o potencial elétrico de um ponto do plano , as curvas de nível de são chamadas curvas equipotenciais, porque nelas todos os pontos têm o mesmo potencial elétrico. Esboce algumas curvas equipotenciais de
onde é uma constante positiva.
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Para essa questão, vamos encontrar algumas curvas de níveis que determinam os pontos onde o potencial elétrico são os mesmos.
Ok, mas como podemos fazer isso?? 🤔🤔
Para determinar as curvas de níveis de uma função, devemos seguir alguns passos. O primeiro, é substituir por uma variável . Essa variável está relacionada com o nível que vamos calcular.
Calcular a curva de nível de uma função é muito parecida com a elaboração de um desenho topográfico em geografia, lembra?
determina a altura do plano que queremos, e todos os pontos que fazem parte dessa altura, fazem parte também da nossa curva de nível.
Temos também e que são constantes positivas, onde podemos determinar qualquer valor positivo a elas.
Passo 2
O primeiro passo é substituir por
Organizando a equação um pouco mais podemos achar o seguinte.
Isolando de um lado da igualdade, temos
Encontramos que as curvas equipotenciais são circunferências de raio
Passo 3
Vamos determinar e , para esboçar algumas curvas
Para o nível , temos
Encontramos uma circunferência de raio .
Para o nível , temos
Encontramos uma circunferência de raio
Para o nível , temos
Encontramos uma circunferência de raio
Passo 4
Observe que o raio sempre deve ser maior ou igual a zero, caso contrário, a curva não existe. Dessa forma
Tirando a raiz dos dois lados para eliminar a potência
A curva de nível vai ser definida quando for maior ou igual a .
Plotando as curvas que encontramos anteriormente, temos
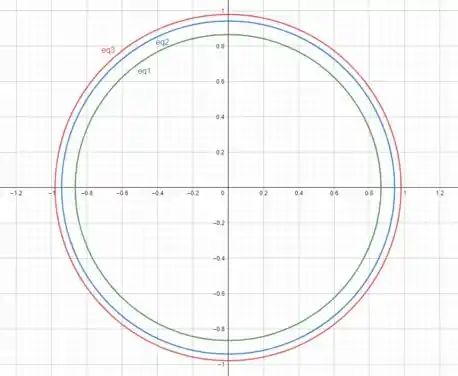
Onde é o nível , é o nível e é o nível .
É isso! Essa resolução te ajudou? Responde Aí! ✌
