Considere . Determine:
- O domínio de ;
- As curvas de nível e o gráfico de ;
Passo 1
a)
Essa é tranquila! A única expressão que poderia causar nessa função é o logaritmo, porque o termo dentro dele tem que ser estritamente positivo.
Mas, no caso, esse termo é .
O único ponto em que é a origem! Portanto, o domínio de é todo o menos a origem.
Passo 2
b)
Pra achar as curvas de nível, temos que igualar a função a uma constante qualquer :
Vamos nos livrar desse logaritmo fazendo:
O termo é constante, portanto temos a equação de um círculo! Ele é centrado na origem e tem raio :
Passo 3
Agora só resta esboçar as curvas de nível! Pro nível por exemplo temos uma circunferência de raio :
Pro nível o raio vale , pro nível ele vale , assim sucessivamente podemos obter vários níveis. Tudo bem que alguns valores como são difíceis de determinar de cabeça. Aqui é fundamental lembrar que vale mais ou menos .
Enfim, o mapa de contorno é uma sucessão de circunferências cujo raio vai aumentando conforme subimos de nível. Ele vai ficar assim:
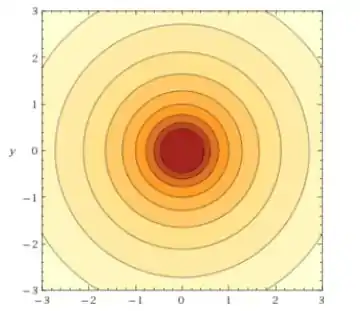
Passo 4
Agora vamos pro gráfico!
As curvas de nível vão ser uma grande ajuda pra gente esboçar esse gráfico. Temos sempre que ter em mente que elas são “fatias” do gráfico. É como se você pegasse uma faca e cortasse o gr��fico em várias alturas na horizontal.
Enfim, além disso a gente tem a maneira mais oficial de visualizar o gráfico pra poder esboçá-lo, que é analisando as suas interseções com os planos coordenados.
Então vamos fazer isso!
Passo 5
Vamos começar lembrando o que já fizemos, que foi zerar a variável ! Lembra? A curva de nível da função nada mais é que a interseção do gráfico com o plano !
E obtivemos
a equação de um círculo de raio centrado na origem.
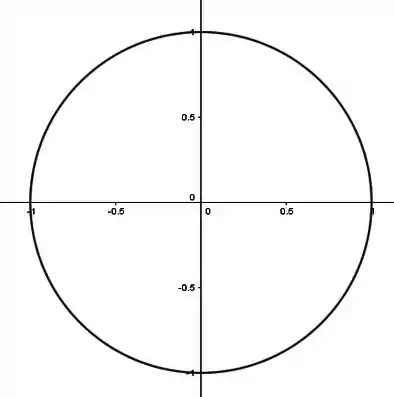
Passo 6
Agora vamos zerar o :
Pelas propriedades do logaritmo, temos
Portanto, a interseção do gráfico com o plano tem equação
E se você sabe esboçar o gráfico da função essa daí não é nenhum problema: basta dobrar os valores. Saca só:
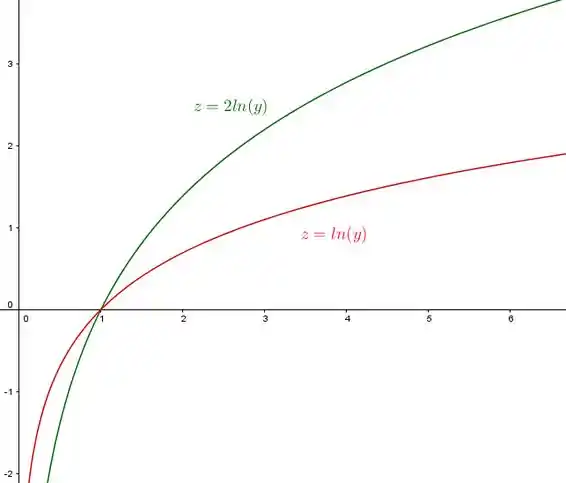
Passo 7
E no plano , zerando a variável , vamos ter a mesma coisa!
Passo 8
Show, agora temos todos os elementos necessários pra fazer um bom esboço!
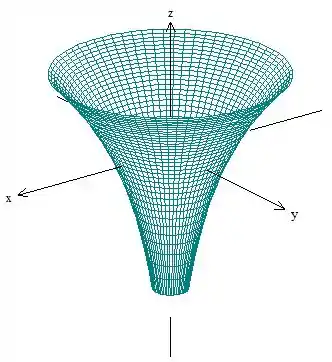
Então é mão na massa! Lembrando da cara do mapa de contorno e das interseções com os planos coordenados, obtemos o gráfico:
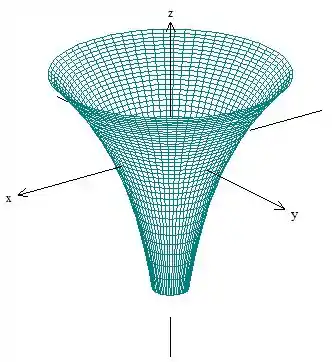
Resposta
a) Domínio: todo o menos a origem
b)
Mapa de contorno:
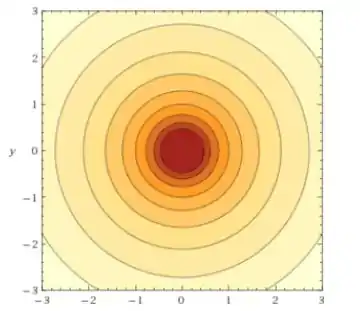
Gráfico: