Considere a função .
- Encontre o domínio e a imagem de .
- O gráfico de é uma quádrica? Se a resposta for sim, identifique a superfície e esboce o gráfico de .
- Identifique as curvas de nível da função e esboce um mapa de contorno. Explique a relação entre o mapa de contorno e o gráfico de .
Passo 1
Fala povo! Essa primeira letra é tranquilinha. Bem, a gente sempre pode entender uma função como uma máquina que transforma entradas em saídas. Nesse caso, em:
Temos as entradas do tipo e e a saída . Se o domínio é o conjunto de entradas possíveis e não existe nenhuma raiz de número negativo, temos que impor a condição:
De forma que o domínio vira então o conjunto de valores que tornam isso verdade, isto é:
Agora, a imagem da função vai ser o conjunto de saídas que a função consegue entregar. Como não existe raiz par que resulte em número negativo, vamos ter:
Passo 2
Agora, será que a curva de é uma quádrica? Pra ter certeza disso, a primeira coisa a se fazer é considerar e ir manipulando:
Eliminando a raiz, temos:
Ta começando a parecer uma em! Como algumas quádricas tem um do lado direito e o único número aí é um , vamos dividir os dois lados da equação por pra fazer esse aparecer:
Multiplicando os dois lados por , temos:
Passando os termos de pro outro lado, temos:
E isso sim tem cara de uma quádrica! Pra padronizar ainda mais, isso é o mesmo que:
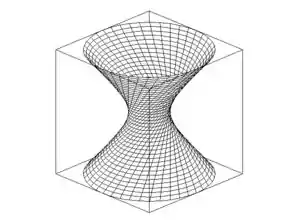
O que é uma equação de um hiperboloide de uma folha, orientado com a abertura ao longo do eixo , como a imagem genérica abaixo:
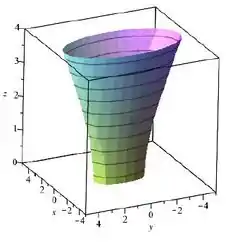
Agora, note que partimos de . Então não queremos essa imagem inteira. Ela tá certa também em relação ao centro, que segundo o nosso modelo vai ser mesmo! Pra fechar nosso esboço, além de remover a parte de baixo, temos que achatar um pouquinho ela pra considerar o efeito das constantes que ficam em baixo de cada eixo, resultando nesse cara simpático aqui como um esboço legal:
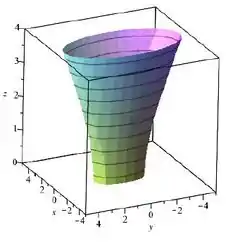
Passo 3
Agora bora falar das curvas de nível. Bem galera, a gente não viu juntos que a superfície se projeta no eixo positivo? Oras, o que são então as curvas de nível se não cortes em alturas diferentes de ? Vamos representar essas curvas de nível como projeções no plano desses cortes. Ok? Definindo então:
Com , afinal, ele deve estar dentro da imagem do hiperboloide, temos:
Se dividirmos tudo por:
Achamos:
E olha só! Isso é exatamente a equação genérica de uma elipse centrada na origem, onde:
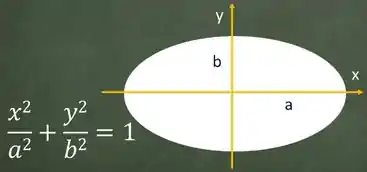
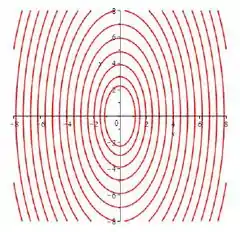
Como o formato da elipse depende de , que é a altura do corte, chegamos a conclusão que as curvas de nível vão ser elipses com formatos variáveis, e podemos juntar todos numa imagem nesse esboço aqui:
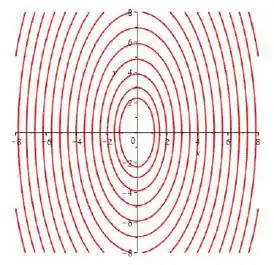
OBS: Note que independente de quem seja , afinal . Por esse motivo, as elipses estão mais espichadas na direção do eixo
Resposta
Sim, a superfície é de uma quádrica, mais especificamente um hiperboloide de uma folha orientado com abertura na direção do eixo , centrado na origem e com . Os esboços da superfície e de suas curvas de nível são: