UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 7a.
7- Dada a função , pede-se:
a) As equações das curvas de nível , e .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Para essa questão, foi dada a função e temos que calcular algumas curvas de níveis. Ok, mas como fazemos isso? 🤔
Calcular uma curva de nível de uma função é como se fizéssemos um corte paralelo ao plano a uma altura .
Algo muito parecido com os desenhos topográficos de geografia, lembra?
Inicialmente temos uma função tridimensional, quando calculamos a curva de nível dessa função, transformamos ela em uma função bidimensional já que estamos transformando a variável em uma constante .
O primeiro passo para se calcular a curva de nível de uma função é substituir por
Organizando um pouco mais essa equação, temos
Essa equação nos lembra muito a equação da circunferência, onde nosso .
Passo 2
Depois de termos organizado a questão, vamos substituir os valores de , e .
Para o nível
Para este nível, temos uma circunferência de raio .
Para o nível
Encontramos uma circunferência de raio .
Para o nível
Encontramos uma circunferência de raio .
Passo 3
Por fim, plotamos as curvas de níveis no plano cartesiano
Onde é o nível , é o nível e é o nível .
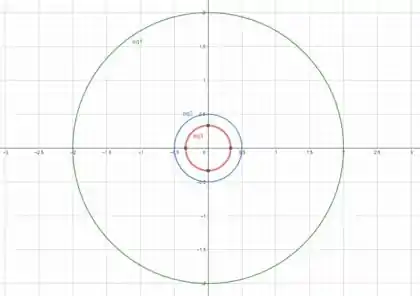
Vemos que quanto maior o nível, menor o raio da circunferência
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
Para ,
Para ,
Para ,