Considere a função
a) Encontre o domínio e a imagem de .
b) O gráfico de é uma superfície quádrica? Se a resposta for sim, identifique a superfície e esboce o gráfico de .
c) Identifique as curvas de nível da função e esboce um mapa de contorno. Explique a relação entre o mapa de contorno e o gráfico de
Passo 1
a) Pensar em domínio de uma função é olhar para expressão dela e ver se tem denominador, raiz par ou log. Se tiver, a gente usa essas restrições aqui para criar inequações que descrevem nosso domínio:
E como a gente tem uma função de duas variáveis, nosso domínio deve ser uma região no plano , tá? Vamos lá!
Vemos que nossa função tem uma raiz par, esse argumento não pode ser negativo
Mas repara que temos dos termos elevados ao quadrado somados, então eles sempre serão positivos. Essa inequação não vai ser uma restrição de fato.
Então, como não temos restrições, nosso domínio é todo o .
Essa é a região onde nossa função está definida.
Passo 2
A imagem é o intervalo de valores de que nossa função assume.
Para determinar isso, gente vai fazer algo parecido ao passo anterior. Vamos olhar nossa função para ver se tem essas características:
A gente vê que a nossa função tem uma raiz par. Aí a gente pode escrever:
Aí vamos fazer aparecer a nossa função aí nessa inequação. A gente pode subtrair 2 dos dois lados
Prontinho, apareceu a expressão da nossa função ali na esquerda. Aí a gente diz que
Aí nossa função assume os valores no intervalo
Passo 3
b) Para a gente testar se o gráfico é uma quádrica, precisamos igualar a e dá aquela rearrumada
Temos que todos os termos estão ao quadrado e positivos. E o termo em está isolado. Então dizemos que temos sim uma quádrica, mais precisamente, um cone.
Passo 4
Vamos esboçar esse cara. Primeira coisa é lembrar da imagem
Então nossa função só existe acima de .
Vimos que isso é um cone. Se a gente olha para expressão original da função
Percebemos que isso vai ser a parte de cima de um cone, com eixo paralelo ao eixo . Essa é a nossa equação que a gente achou
Comparando com a equação que achamos com a geral do cone para esse caso
Essa superfície está centrada em . Ah e aquele do lado do , mostra que a interseção entre a superfície e o plano vai uma elipse
Aí esboçando a parte de cima desse cone que está deslocado para baixo, começando de , temos
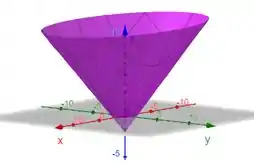
Passo 5
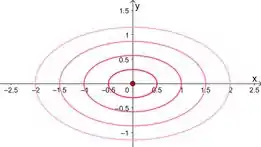
c) Para achar as curvas de nível, a gente precisa igualar nossa função , a valores constantes que a gente chama de .
E analisar que curvas essas expressões formam.
Mas como , temos também que
Aí nossa função é
As curvas de nível ficam
Passo 6
Agora a gente analisa essa expressão para alguns intervalos de . Uma dica é ver onde esse lado esquerdo (onde só temos as constantes) vai zerar, porque aí a gente consegue marcar uns intervalos interessantes
Como , temos os intervalos
Passo 7
Vamos olhar o que acontece em :
A única coisa que satisfaz essa equação é o ponto .
Por fim, para .
Nesse caso, esse termo da esquerda vai ser positivo, podemos testar isso fazendo por exemplo.
Então essas são elipses.
Passo 8
Aí agora é variar esse e fazer várias curvas no plano . Tendo em vista que a gente precisa representar esses intervalos onde elas são diferentes
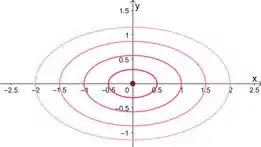
Aí a gente pode interpretar essas curvas como as projeções em das interseções entre a nossa função e os planos . É como se a gente tivesse vendo como é o nosso gráfico, visto de cima, em alturas .
Resposta
a)
b) cone
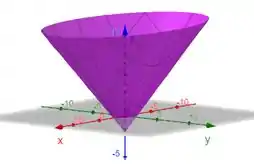
c) , a origem
elipses