UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 2c.
Esboce o gráfico das funções a seguir:
c)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Para essa questão, foi solicitado que esbocemos um gráfico de , mas você acha que podemos fazer isso? 🤔
Esboçar um gráfico é traçar, de uma forma mais material, a imagem da função.
Uma função está contida em 3 dimensões, ou seja, dependendo de um determinado ponto em e um determinado ponto em , vamos ter uma imagem em , com isso, podemos afirmar que na verdade .
Podemos comparar com uma lei muito famosa, a chamada 3° Lei de Newton ou lei da Ação e Reação. Essa lei da natureza diz que para cada ação, há uma consequência, por exemplo, se chegarmos em casa muito tarde, nossas mães vão ficar preocupadas, não é?
Então, nossas ações são nossas variáveis e , no caso, chegar em casa tarde. Quando isso acontece, temos uma reação, ou seja, nossa variável ou , que no caso foi deixar nossas mães preocupadas.
Entendeu? Para cada valor de e , vamos ter um (para cada ação, vamos ter uma reação)!
Passo 2
Na prática, funciona da seguinte maneira:
Temos a função que vamos esboçar o gráfico
O próximo passo é analisarmos o que esperamos de como será o gráfico.
Neste caso, como você acha que ele vai ser? Plano, ondulado, inclinado, curvo...?
Podemos esboçar um gráfico construindo ele parte por parte.
Usando a analogia que descrevemos anteriormente, podemos estimar as consequências (os valores de ou de ), a partir das causas que vamos estipular (os valores de e ).
Podemos fazer isso construindo uma tabelinha com os valores estimados para , o que vai nos resultar em um gráfico e o mesmo para que vai resultar em um gráfico . Por exemplo.
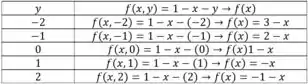
Com isso, em cada plano correspondente ao valor estimado perpendicular a , vamos ter um gráfico.
Passo 3
Seguimos os mesmos passos para esboçar
Plotando as funções que calculamos em 3 dimensões, cada um em um plano correspondente, por exemplo, em , e assim por diante, temos
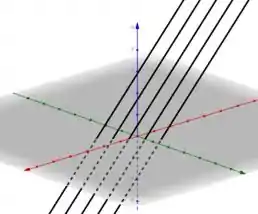
Traçando um plano que contém todas as retas, vamos ter nosso gráfico de que estávamos buscando.
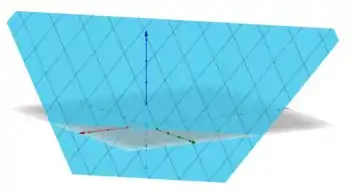
O plano azul, é o gráfico de !
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
Gráfico no Último Passo