UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 2h.
Esboce o gráfico das funções a seguir:
h)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Para essa questão, foi solicitado que esbocemos um gráfico de , mas você acha que podemos fazer isso? 🤔
Esboçar um gráfico é traçar, de uma forma mais material, a imagem da função.
Uma função está contida em três dimensões, ou seja, dependendo de um determinado ponto em e um determinado ponto em , vamos ter uma imagem em , com isso, podemos afirmar que na verdade .
Podemos comparar com uma lei muito famosa, a chamada 3° Lei de Newton ou lei da Ação e Reação. Essa lei da natureza diz que para cada ação, há uma consequência, por exemplo, se depois de uma vídeo aula aqui no Responde Aí, a gente não fazer exercícios pra exercitar o que acabamos de aprender, vamos ter mais dificuldades na prova, não é?
Então, nossas ações são nossas variáveis e , no caso, não fazer exercícios. Quando isso acontece, temos uma reação, ou seja, nossa variável ou , que no caso foi ter dificuldades na prova.
Entendeu? Para cada valor de e , vamos ter um (para cada ação, vamos ter uma reação)!
Passo 2
Na prática, funciona da seguinte maneira:
Temos a função que vamos esboçar o gráfico
O próximo passo é analisarmos o que esperamos de como será o gráfico.
Neste caso, como você acha que ele vai ser? Plano, ondulado, inclinado, curvo...?
Dentro da raiz de temos algo muito parecido com a equação da elipse
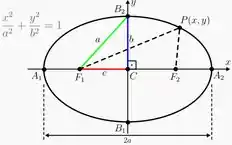
Nesses casos, podemos esboçar o gráfico pelo método da curva de nível, método muito parecido com os desenhos de topografia em geografia.
Este método consiste em cortar o gráfico em planos perpendiculares a , fazemos isso substituindo por na equação, com isso, temos
Organizando essa equação para ficar mais parecida com a equação da elipse, primeiro elevando os dois lados ao quadrado para eliminar a raiz.
Dividindo os dois lados por
Portanto, seguindo a equação da elipse, e
Passo 3
Para cada plano em , vamos ter uma elipse diferente.
Desenhando a equação que encontrarmos no plano que foi calculado, vamos ter uma curva de nível.
Vamos tabelar alguns valores e plotar em três dimensões
Perceba que não podemos usar valores negativos para , pois , a raiz está com sinal positivo (mesmo que esteja oculto), se estivesse estaríamos buscando apenas os valores negativos. Então não queremos os valores negativos de .
Em , e é negativo, isso é impossível no conjunto dos números reais, então neste plano, a função está indefinida.
Em , e é zero, isso representa um ponto.
Nos demais níveis, são representadas elipses, onde plotando elas em três dimensões, temos
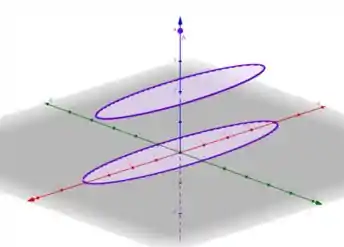
Por fim, com base nas curvas de níveis, ligamos as curvas que plotamos formando um plano que será nosso gráfico
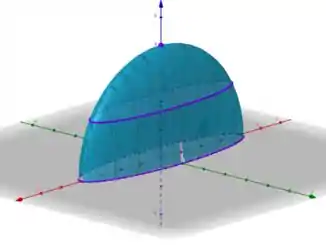
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
Gráfico no último passo.