UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 3a.
Considere as funções:
a) . Para quais valores de e temos ? Represente graficamente a resposta.
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
O que essa questão está pedindo pra nós? Ela quer que encontremos a relação de e para que seja igual a e representar a resposta graficamente.
Dizer que , é sair de três dimensões para duas, já que você está definindo uma constante na 3° dimensão.
Isso significa que vamos ter uma relação ou , onde e .
A partir dessa relação, vamos ter os requisitos necessários para obter os valores de e para que seja igual a .
A partir dessas ideias, vemos que o problema exige uma certa afinidade com funções e essa afinidade é fundamental! Então bora lá praticar!
Passo 2
O método de resolução desasa questão é muito parecida com o método das curvas de níveis para encontrar o gráfico de , a diferença é que no caso, usamos apenas um nível.
O método das curvas de níveis consiste em substituir por e definir níveis da função substituindo por uma constante que representa níveis de .
Algo muito parecido com a elaboração de um desenho topográfico em geografia.
Neste caso, temos
Isolando , temos uma função mais fácil de ser reconhecida.
Imagine que
Melhorou? Graficamente é mais simples de visualizar assim.
Com isso, vemos que e pode ser qualquer número real, desde que ou !
Passo 3
Podemos obter o gráfico determinando alguns valores para e pontuando no plano cartesiano, por exemplo
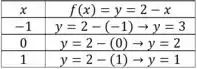
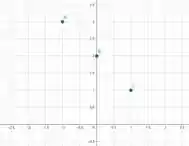
Plotando os pontos , e no plano cartesiano, temos
Ligando os pontos por uma reta, temos
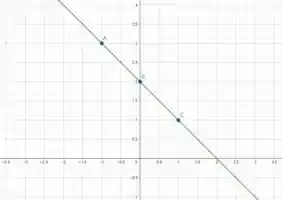
Esse é o gráfico de .
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí