Faça o esboço do mapa de contorno e do gráfico da função e compare-os.
Passo 1
Vamos começar determinando as curvas de nível, igualando a função a uma constante qualquer :
Repare que isso é a equação de uma elipse! Podemos botá-la na forma tradicional
Passo 2
Dividindo tudo por :
É a equação de uma elipse centrada na origem, e cujos semieixos valem e .
Portanto, o mapa de contorno da função basicamente vai ser um monte de elipses de vários tamanhos, e que respeitem a condição que o semieixo horizontal é 3x maior que o vertical.
Passo 3
Por exemplo, com , temos a elipse
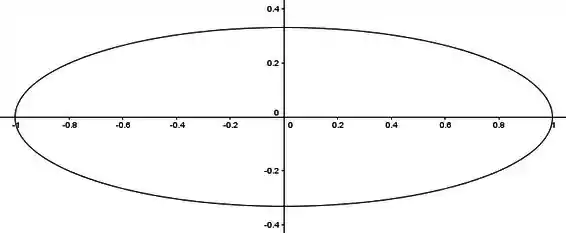
Passo 4
A questão pediu apenas o mapa de contorno, ela não exigiu especificar a equação de cada curva de nível e tal. Então mano, é só mandar bala e desenhar várias elipses respeitando essas proporções!
O que vai dar no mapa de contorno:
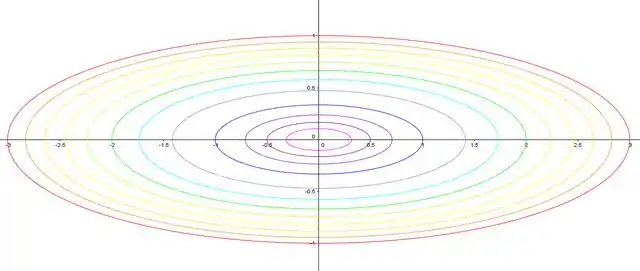
Obs: se empolgar e desenhar as curvas de nível nas cores do arco-íris é facultativo.
Passo 5
Agora ele quer o gráfico da função. É nessa hora que a gente chama de pra chegar na equação de uma superfície:
Aí agora ou você é o(a) mito das quádricas, bate o olho e já vê de cara que se trata de um paraboloide elíptico, ou você dá uma olhada no mapa de contorno da função e chega numa conclusão parecida.
Pra confirmar ainda podemos seguir o procedimento padrão e zerar as variáveis, vendo como são as interseções da superfície com os planos coordenados.
Passo 6
Fazendo , temos, no plano :
que é uma parábola.
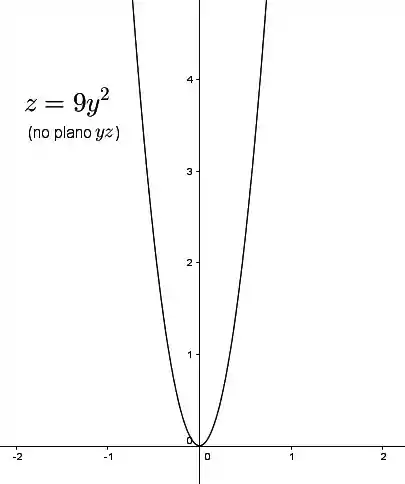
Passo 7
E fazendo , temos, no plano :
que, vejam só, também é uma parábola!
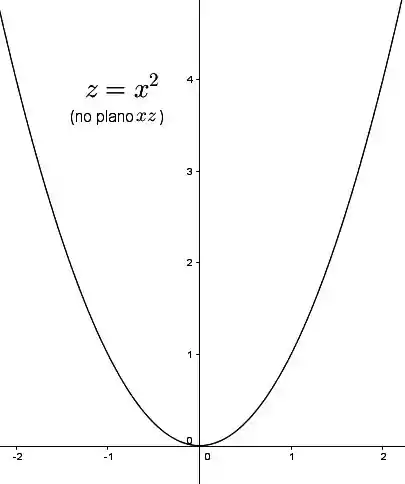
Passo 8
Resumindo, nossa superfície vai ser a junção de um monte de parábolas voltadas pra cima e com vértice em . Sendo que se cortarmos ela horizontalmente, temos que observar as elipses do mapa de contorno.
Então lá vai o gráfico:
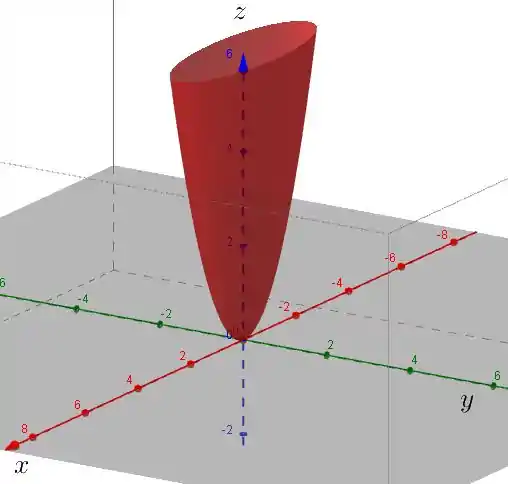
Passo 9
Calma que ainda não acabou! Ele ainda quer que a gente compare o mapa de contorno com o gráfico... o que é meio idiota já que nos baseamos no mapa de contorno pra fazer o gráfico!
Enfim, aqui eu diria algo do tipo “eles são coerentes um com o outro, as curvas de nível são elipses, o gráfico é um paraboloide elíptico, faz total sentido, blablabá”. Algo do tipo. Afinal, você é universitário(a), eu confio no seu poder de enrolation! ;)
Resposta
Mapa de contorno:
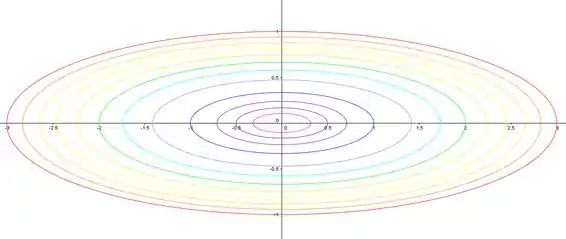
Gráfico:
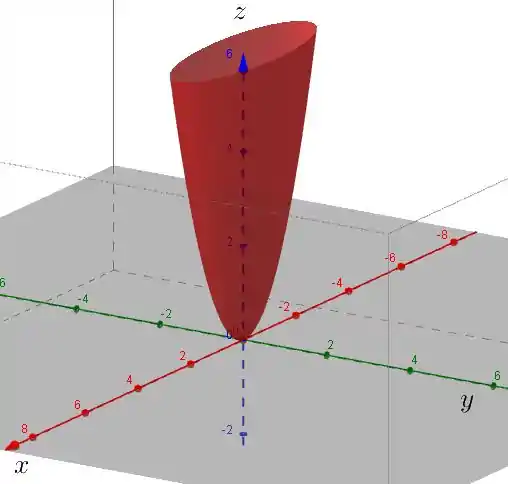
Eles são coerentes entre si, a partir de um podemos visualizar o outro.