9 - Associe a função com seu gráfico (indicado por na Figura 1) e com suas respectivas curvas de nível (indicado por na Figura 2).

a)
b)
c)
d)
e)
f)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Para essa questão, vamos usar nossos conhecimentos em curvas de níveis. Para cada função que foi dada, temos que calcular as suas curvas de níveis para relacionar com os gráficos da figura e as curvas de níveis da figura 2.
Tem ideia de como podemos fazer isso?? 🤔🤔
Calculamos as curvas de níveis substituindo pelos níveis que queremos. Após essa substituição, plotamos os gráficos no plano e comparamos com as curvas de níveis dadas na figura 2, aquela que mais se parecer, será a curva de níveis que estaremos buscando. Depois disso, se com base apenas nas curvas de níveis não for possível determinar seu gráfico, podemos plotar as curvas de níveis nos níveis que foram calculados e imaginar seu gráfico.
Bora analisar uma função de cada vez!
Passo 2
A função a), temos
Podemos multiplicar os dois lados da equação por para tirar o de um dos lados da equação.
Assim podemos cortar o com o .
Elevando os dois lados ao quadrado para eliminar a raiz
Essa equação é exatamente de uma circunferência onde . Assim no nosso caso o raio é .
Obtendo as curvas dos níveis , , e
Este termo é adicionado no resultado, pois a cada período o valor se repete.
Plotando essas curvas no plano , temos
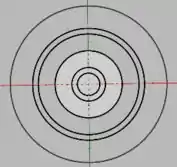
Comparando com as curvas da figura 2, vemos que temos apenas um gráfico que contem circunferências centradas na origem, no caso, a figura . Com o , as curvas em três dimensões e ligando as curvas de níveis, podemos imaginar a curva como sendo
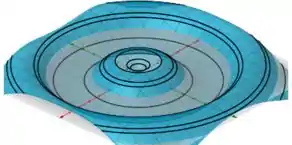
Dentre as curvas da figura 1, a que mais se assemelha é o gráfico . Portando, a função a) é representada pelo grafico e pelas curvas .
Passo 3
A próxima função é a b), dada por , podemos escreve-la também como
Podemos isolar de um lado da equação, como
Multiplicando os dois lados por para eliminar o , temos
Para essa função, temos que ter o auxilio de ferramentas para plotar as curvas, já que a função não é nem um pouco intuitiva.
Para os níveis , , , , e . Temos as curvas como
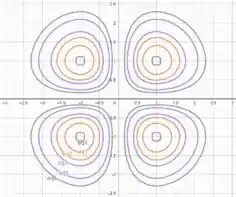
Comparando com as curvas da figura 2, vemos a semelhança entre nosso resultado e a figura .
A partir da análise das curvas de níveis, vemos que temos 4 protuberâncias, uma em cada quadrante.
Comparando essa afirmação com os gráficos da figura 1, podemos dizer que o gráfico , encaixa no nosso problema, confirmando que
Passo 4
Para a função c), temos , essa é bem mais tranquila. Podemos escreve-la como
Essa equação é muito parecida com uma equação de elipse
Não precisamos nem plotar as curvas de níveis dessa função, já que temos apenas uma figura que contém elipses que se encaixam na descrição da nossa função. No caso a figura da figura 2.
Vemos que quanto maior o nível , menor será nossa elipse, com isso, podemos imaginar o gráfico dessa função como sendo quase como um cilindro elíptico com a base mais grossa e afinando conforme aumenta. Analisando a figura 1, temos um gráfico que se encaixa nessa afirmação, no caso a figura

Com isso, podemos concluir que a função c) é representada por
Passo 5
A função d) é dada por
Calculando as curvas e , temos
Para essas curvas, precisamos da ajuda de alguma ferramenta para plotar essas curvas de níveis, já que essa função não é muito trivial.
As curvas de e , tem a seguinte cara
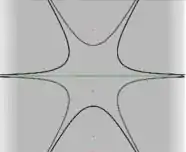
Comparando com as curvas de níveis que temos na figura 2, vemos a semelhança com as curvas da figura , onde temos esse formato de estrela.
Plotando o gráfico da função com base em mais curvas de níveis, encontramos

Agora comparando o gráfico que obtemos com os gráficos dados na figura 1, podemos perceber a semelhança com o gráfico , portanto.
Passo 6
A função e) foi dada como
Com o auxílio de uma ferramenta para plotar as curvas de , , , e .
Com isso, obtermos as seguintes curvas de níveis

Comparando as curvas que tenho aqui com as curvas dadas na figura 2, vemos a semelhança entre as curvas , onde temos esses quadrantes com curvas arredondadas dentro.
Com base nas curvas de níveis podemos plotar o gráfico da função e)
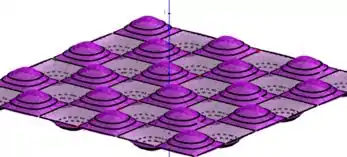
Comparando nosso resultado com os gráficos apresentados na figura 1, podemos notar a semelhança entre o gráfico , onde temos algo parecido com uma caixa de ovos. Logo:
Passo 7
Por fim, a função f) é dada como .
Novamente vamos precisar de um auxílio para plotar as curvas , , e . Com isso, obtemos as curvas
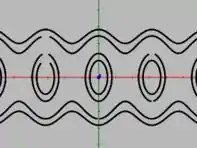
Comparando essas curvas com as curvas dadas na figura 2, podemos ver a semelhança entre nosso resultado e as curvas , onde temos algumas elipses e algumas ondas.
Com base nessas curvas de níveis, podemos plotar o gráfico f), tal que temos
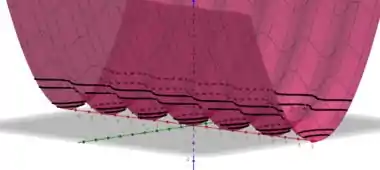
Comparando os gráficos da figura 2, podemos ver que o gráfico de se parece com o nosso resultado. Onde temos uma superfície ondulada, como se fosse uma telha. Logo:
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍