UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 4a.
3- Desenhe as curvas de nível das funções de duas variáveis a seguir para os valores de dados:
a) ;
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Para essa questão vamos calcular as curvas de níveis de . Ok?
Mas peraí! Como fazemos isso?? 🤔
Para calcular as curvas de níveis de uma função temos que imaginar que estamos “cortando” a função em alturas diferentes, algo muito parecido com desenhos topográficos em Geografia.
O primeiro passo é substituir por .
Esse representa a altura de corte com relação ao plano .
Esse tipo de questão costuma ter uma resolução bem rápida, então sem mais delongas podemos partir para resolver a questão!
Passo 2
Como dizemos antes, o primeiro passo é substituir por , ou seja
Agora vamos substituir pelos valores solicitados
Para
Isolando de um lado, temos
Encontramos que em , .
Essa função é bastante conhecida, mas se não estiver tão claro, podemos usar o método do tabelamento para substituir em para encontrar o valor em , obtendo assim um ponto no plano cartesiano, por exemplo
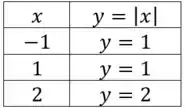
Obtemos os pontos , e .
Vamos guardar estes pontos que já voltamos pra eles.
Passo 3
Para
Isolando de um lado, temos
Tirando a raiz dos dois lados para tirar a potência de
Usando o método da tabelinha, vamos encontrar os pontos que contém a função
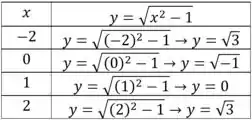
Analisando a função, sabemos que raiz de numero negativo não existe nos números reais, então , e isso não acontece quando .
Portanto no intervalo a função é indefinida.
Obtemos os pontos , e .
Já já vamos plotar esses pontos.
Passo 4
Para
Isolando o , temos
Tirando a raiz dos dois lados para tirar a potência de
Temos o mesmo problema anterior, dentro da raiz não pode ser negativa, então
Obtendo os pontos para esboçar o gráfico deste nível, temos
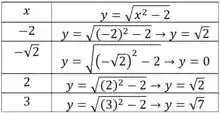
Com isso obtemos os pontos , , e .
Vamos guardar estes pontos também.
Passo 5
Para
Isolando o , temos
Tirando a raiz dos dois lados para tirar a potência de
Da mesma forma, dentro da raiz não pode ser negativo, então .
Obtendo pontos a partir do método da tabelinha, temos
Obtemos , e
Agora vamos plotar estes pontos em um plano cartesiano.
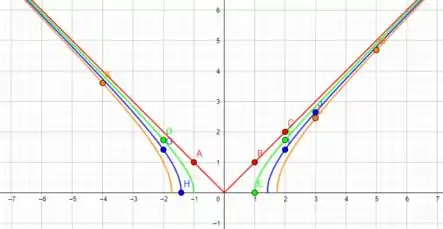
Passo 6
Temos , e para , , , para , , , e para e , e para .
Plotando esses pontos no plano , temos
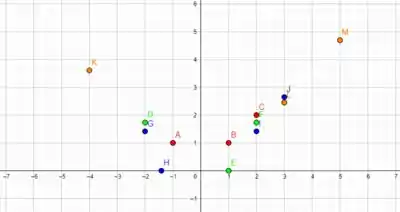
Ligando os pontos de cada nível , vamos obter as curvas de níveis que estamos procurando.
Caso alguma curva não esteja tão clara, podemos obter mais pontos no método da tabelinha.
Por fim, as curvas de níveis, vão ser
Fim! Iae, o que achou? Responde Aí! 😁
Resposta
,
,
,
,