UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 5.
Uma camada fina de metal, localizada no plano , tem temperatura no ponto . As curvas de nível de são chamadas de isotérmicas porque todos os pontos em uma isotérmica têm a mesma temperatura. Faça o esboço de algumas isotérmicas se a função de temperatura for dada por
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Temos aqui uma típica questão de aplicação de curvas de níveis.
O enunciado diz que temos uma camada fina de metal no plano . Foi dada uma função que representam as temperaturas do metal.
As curvas de níveis de são os pontos em que o metal tem a mesma temperatura.
O objetivo principal da questão é esboçar algumas curvas de níveis da função .
Ok, mas como eu calculo as curvas de níveis de uma função? 🤔
Imagine que você tem uma função e você corta essa função em uma altura do plano . A curva de nível é a curva que se forma no plano de corte que fizemos, algo muito parecido com desenhos topográficos em geografia, lembra?
A primeira coisa a se fazer é, no caso, substituir por . Com isso vamos transformar uma função tridimensional em bidimensional.
Com essas ideias, podemos iniciar os cálculos.
Passo 2
Primeiro de tudo, substituímos por
Vamos organizar essa equação um pouco mais.
O próximo passo é substituir por valores quaisquer, mas observe que pois se for , resultará em uma indeterminação e se for menor que , o lado direito da igualdade será negativo.
Observando a equação que temos, vemos que se trata da equação de uma elipse, onde
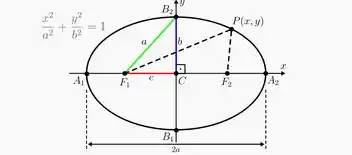
Logo se o lado direito da equação não admite valores negativos
Passo 3
Vamos definir alguns níveis de e .
Agora substituindo os valores de na equação, temos
Para
Encontramos uma elipse de e
Para
Encontramos uma elipse de e .
Para
Encontramos uma elipse de e
Por fim, para
Encontramos uma elipse de e
Passo 4
Só o que falta é plotar os gráficos das curvas que encontramos, que ficam da seguinte maneira.
representa a curva de nível , representa a curva de nível , representa e representa .
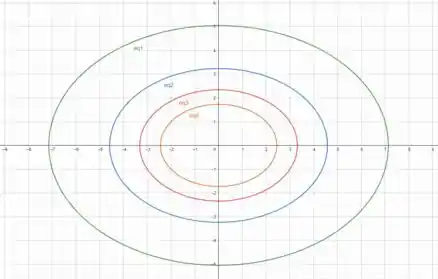
Cada uma das curvas representa pontos onde a temperatura é a mesma, ou seja, qualquer ponto na curva 1 tem a mesma temperatura, assim como na curva 2, 3 e 4.
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
Para ,
Para ,
Para ,
Para ,