UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 7b.
7- Dada a função , pede-se:
b) A equação e o esboço da curva de nível que contém o ponto .
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Para essa questão foi dada uma função e temos que encontrar a curva de nível que contém o ponto . Parece difícil?
Curvas de níveis de uma função são obtidas a partir do corte na função a uma altura do plano , formando uma curva correspondente à curva de nível na altura .
Algo muito parecido com desenhos topográficos em Geografia.
O primeiro passo a se fazer é substituir por
Organizando um pouco mais essa equação, temos
Encontramos uma equação de circunferência que representa as curvas de níveis de
Passo 2
Temos que encontrar a curva de nível que contém o ponto , mas como vamos achar este nível?
Se representa o nível que queremos, basta substituirmos por e por que vamos encontrar um valor pra , este valor será o nível que contém este ponto. Veja só
Com isso, encontramos que no nível a curva de nível de passará pelo ponto
Substituindo o valor de na equação de curva de nível, vamos ter a equação que representa o nível que procuramos
Passo 3
Esboçando a curva que encontramos no plano cartesiano, temos uma circunferência, centrada na origem, de raio .
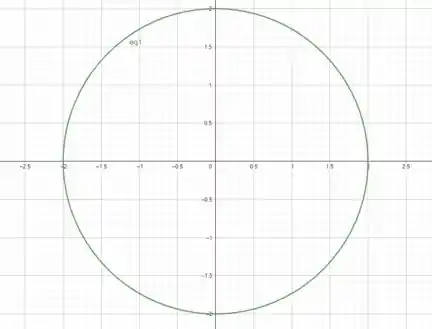
Fim! Iae, o que achou? Responde Aí! 😁