UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 4b.
3- Desenhe as curvas de nível das funções de duas variáveis a seguir para os valores de dados:
b) ;
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Para essa questão, temos que calcular as curvas de níveis para . Mas peraí, curvas de níveis? O que é isso? 🤔
Quando temos uma função e queremos descobrir suas curvas de níveis, estamos fazendo um corte paralelo ao plano a uma altura .
Já viu um desenho topográfico em geografia? É praticamente a mesma ideia.
Para calcular uma curva de nível, temos uma função tridimensional e vamos converte-la para uma função bidimensional substituindo por e posteriormente pelo nível que desejamos conhecer.
Com essas ideias, podemos iniciar nossos cálculos.
Passo 2
Primeiro de tudo, vamos substituir por
Isolando , vamos obter uma função bidimensional.
Tirando a raiz dos dois lados para obter , temos
Agora só substituir pelo nível que queremos e partir pra galera!
Para , temos
Essa função é muito famosa, mas caso não consiga visualizar a curva que é formada, podemos usar o método da tabelinha.
Este método consiste em fazer uma tabela substituindo um valor em e calcular o resultado em , assim obtendo um ponto no espaço . Por exemplo
Com isso, obtemos os pontos , e .
Vamos segurar esse ponto por enquanto.
Passo 3
Para , temos
Utilizando o método da tabelinha para obter os pontos em , temos
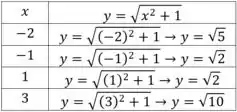
Para este nível , obtemos os pontos , , e .
Para , temos
Obtendo alguns pontos de , temos
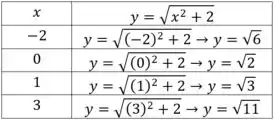
Para , obtemos os pontos , , e
Passo 4
Para , temos
Obtendo os pontos para formar a curva neste nível, temos
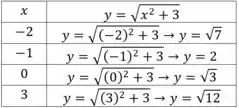
Obtemos , , e
Plotando estes pontos no plano cartesiano, temos
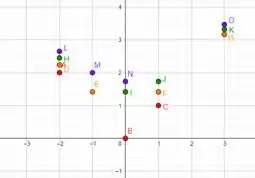
Ligando os pontos de seus níveis, obtemos as curvas de níveis que procuramos
Caso alguma curva não esteja muito clara, podemos adicionar mais valores na tabelinha, assim obtendo mais pontos.
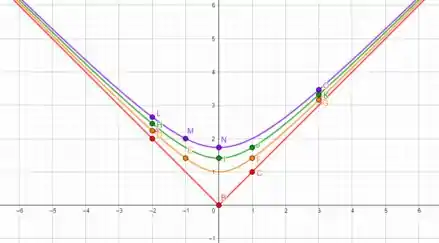
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
,
,
,
,