UFABC. Cálculo. Lista: Funções de Várias Variáveis. Lista 1 - Domínios, Gráficos e Curvas de Nível. 2018.3. Questão: 1F.
Nos seguintes exercícios, encontre o domínio , encontre a imagem , e descreva as curvas de nível da função:
f)
Passo 1
Fala aí, meus queridos! Tudo certinho?
Para resolver essa questão, temos que entender os conceitos de domínio e imagem de uma função.
Podemos dizer que o domínio de uma função é o conjunto de todas as entradas possíveis da função e a imagem é o conjunto de todas as saídas possíveis da função. Ou seja.
Se
Seu domínio será o conjunto dos números reais.
Sua imagem será, também, o conjunto dos números reais maiores que zero, já que qualquer operação com um número elevado por não resulta em zero e números negativos, e menores que , já que linearizando a função, vamos ter.
tem que ser que zero e isso só acontece quando for que 0.
Passo 2
Para descrever a curva de nível de uma função, devemos iguala-la ao nível que queremos, por exemplo, nesse caso vamos usar os níveis , e .
Para o nível
Para o nível
Para o nível
Temos então as seguintes equações:
Agora esboçamos os gráficos dessas equações e teremos os níveis , e .
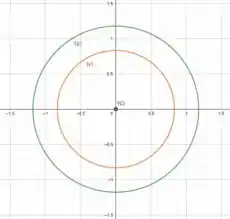
É isso! Entendeu tudo? Responde Aí! 😎👍