Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Funções de 2 variáveis, Curvas de Nível e Gráfico

Ver Teoria
Exercício 44123456789101112131415161718192021222324252627282930313233343536373839404142434546474849505152535455565758596061

Enunciado

UNICAMP – Cálculo 2 – Provas antigas – P1 – 2022.1 – 2

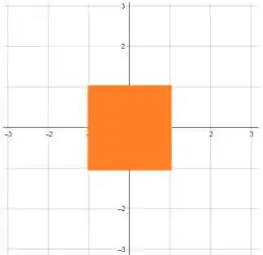
Determine e faça um esboço do domínio da função

f x , y = 1 - x 2 - 1 - y 2

Passo 1

Eaeeee, belezinha??? Seguinte... precisamos determinar o domínio da função de duas variáveis dada por:

f x , y = 1 - x 2 - 1 - y 2

Lembra que o domínio são os valores que x e y podem assumir sem que haja algum problema matemático na função? Então, pra f ( x , y ) , quais que seriam os possíveis pontos de restrição?

Então bora pensar junto aqui... para que f x , y exista, temos 2 termos para isso acontecer:

  1. 1 - x 2 ≥ 0 ;
  2. 1 - y 2 ≥ 0 .

Rearranjando, temos:

  1. 1 - x 2 ≥ 0 ∴ x 2 ≤ 1 ;
  2. 1 - y 2 ≥ 0 ∴ y 2 ≤ 1 ;

Passo 2

Esboçando x 2 ≤ 1 , temos:

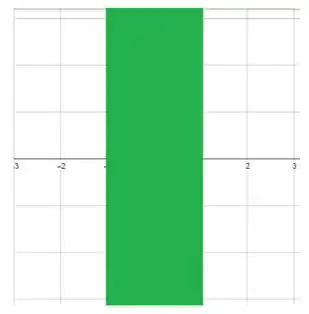
Esboçando y 2 ≤ 1 , temos:

Passo 3

Fazendo a interseção entre as duas regiões, temos:

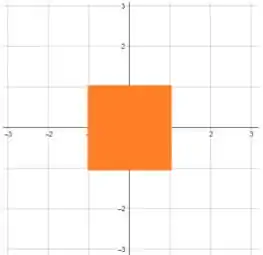
Entendeu direitinho? Responde aee ;)

Resposta

Exercícios de Livros Relacionados

Desenhe as curvas de nível e esboce o gráfico. f (x , y) = 4 x^2 + y ² ²
Utilize um computador para traçar o gráfico da função usando vários domínios e pontos de vista. Imprima a que, em sua opinião, oferece a melhor visão. Se seu programa também produz curvas de nível, tr
Esboce o gráfico da função. f x , y = 4 x 2 + y 2
Utilize um computador para traçar o gráfico da função, usando vários pontos de vista e tamanhos de janela. Comente o comportamento da função no limite. O que acontece quando x e y se tornam muito gran
Faça uma correspondência entre a função (a) e seu gráfico (indicado por A-F na página 828), (b) e seus mapas de contorno (indicado por I-VI). Justifique sua escolha. z = x - y 1 + x 2 + y 2